在信号分析与处理中,频谱分析是重要的工具。FFT(Fast Fourier Transform,快速傅立叶变换)可以将时域信号转换至频域,以获得信号的频率结构、幅度、相位等信息。该算法在理工科课程中都有介绍,众多的仪器或软件亦集成此功能。FFT 实用且高效,相关原理与使用注意事项也值得好好学习。
一、何为 FFT
对于模拟信号的频谱分析,首先得使用 ADC(模拟数字转换器)进行采样,转换为有限序列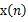 ,其非零值长度为 N,经 DFT(离散傅立叶变换)即可转化为频域。DFT 变换式为:
,其非零值长度为 N,经 DFT(离散傅立叶变换)即可转化为频域。DFT 变换式为:
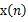 ,其非零值长度为 N,经 DFT(离散傅立叶变换)即可转化为频域。DFT 变换式为:
,其非零值长度为 N,经 DFT(离散傅立叶变换)即可转化为频域。DFT 变换式为: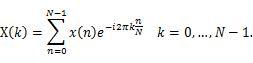
在上式中,N 点序列的 DFT 需要进行 N2 次复数乘法和次复数加法,运算量大。FFT 是 DFT 的快速算法,利用 DFT 运算中的对称性与周期性,将长序列 DFT 分解为短序列 DFT 之和。最终运算量明显减少,使得 FFT 应用更加广泛。
FFT 基于一个基本理论:任何连续的波形,都可以分解为不同频率的正弦波形的叠加。FFT 将采样得到的原始信号,转化此信号所包含的正弦波信号的频率、幅度、相位,为信号分析提供一个创新视觉。
例如在日常生活中有使用到的 AM(Amplitude Modulation,幅度调制)广播,其原理是将人的声音(频率约 20Hz 至 20kHz,称为调制波)调制到 500kHz~1500kHz 正弦波上(称为载波)中 ,载波的幅度随调制波的幅度变化。声音经这样调制后,可以传播得更远。在 AM 的时域波形(波形电压随时间的变化曲线),载波与调制波特征不易体现,而在 FFT 后的幅频曲线中则一目了然。如下图为 1000kHz 载波、10kHz 调制波的 AM 调制信号,时域信号经 FFT 后其频率能量出现在 990kHz、1.01MHz 频率处,符合理论计算。
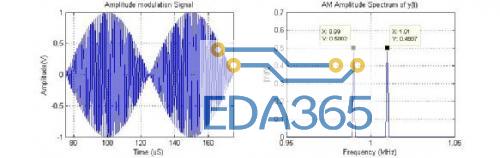
图 1 调制波 10kHz、载波 1000kHz 的 AM 时域与频域曲线
二、FFT 相关知识
现实生活中的模拟信号,大多都是连续复杂的,其频谱分量十分丰富。正如在数学中常量π,其真实值是个无理数。当用 3.14 来替代π时,计算值与真实值就会有偏差。在使用 FFT 这个工具时,受限于采样时的频率 Fs、采样点长度 N、ADC 的分辨率 nbit 等因素的制约,所得到的信息会有所缺失与混淆。
1. 奈奎斯特区与波形混叠
FFT 分析结果中,存在一个那奈奎斯特区的概念,其宽度为采样率的一半 Fs/2,信号频谱被分成一个个相连的奈奎斯特区。日常信号分析中,大多关心的是 1st 奈奎斯特区的信号,即 DC 到 Fs/2 的频段。FFT 所得到的信号频率信息,也是在 1st 奈奎斯特区内。其他高奈奎斯特区频段的信号,会以不同的方式混叠到 1st 奈奎斯特区:
l 偶数奈奎斯特区会镜像后混叠到 1st 奈奎斯特区;
l 奇数奈奎斯特区会频移后混叠到 1st 奈奎斯特区。
如下图所示,假如原有模拟信号频谱段较宽,信号频段的最大频率大于采样率 Fs。在采样率 Fs 下,信号频谱的 A、B、C 三部分区域,分别位于 1st、2st、3st 奈奎斯特区。那经 FFT 后:
lA 部分信号本来就在 1st 奈奎斯特区,保持不变;
lB 部分频谱会以 Fs/2 为镜像后混叠到 1st 奈奎斯特区;
lC 部分频谱频偏 Fs 后混叠到 1st 奈奎斯特区。
这样在 FFT 的分析结果中,1st 奈奎斯特区就会重叠了 A、B、C 三部分区域的信号。其他奈奎斯特区频率信号干扰到需分析的信号,就会造成常说的波形混叠问题。
就单个频率信号而言,若原始信号的频率为|±KFs ±Fin|(K 为自然数),则经过 FFT 分析后,信号会落入在 1st 奈奎斯特区的 Fin 频率处。

图 2 奈奎斯特区投影与波形混叠
这在时域上理解不难:在常用设备示波器的采样率设为 100MSa/s,这时输入 10MHz、90MHz、110MHz 频率的信号,采样得到的波形是一样的,都为 10MHz。此时奈奎斯特区宽度为 50MHz,信号 90MHz 位于 2st 奈奎斯特区,经 Fs/s 镜像后,为 10MHz;信号 110MHz 位于 3st 奈奎斯特区,经频偏 Fs 后,亦为 10MHz。在 FFT 后的数据中,这三个频率信号的频点都落在 1st 奈奎斯特区的 10MHz 处。
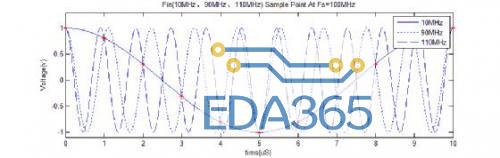
图 3 波形混叠时的时域芯片
为了解决信号混叠问题,可以采取以下措施:
l 提高模数转换器 ADC 的采样率 Fs
这相当把 1st 奈奎斯特区拉宽。当满足 Fs/2 大于信号频段的最大频率 Fin_max 时,自然不会现混叠。这是采样定理的简单实践。
l 在模数转换器前串入抗混叠滤波器
抗混叠滤波器最常见的是低通滤波器,此滤波器可以将高于 Fs/2 的高阶奈奎斯特区频段信号衰减掉,只保留待测量 1st 奈奎斯特区频段的信号。
2.FFT 数据的物理意义
长度为 N 的有限序列,经 FFT 后得会到 N 个复数,完成了时域到频域的涅磐。原始信号包含的各种正弦信号,会转化成对应位置的复数:
l 第一个复数,代表信号的直流分量。此复数的模值,为直流分量的 N 倍。
l 第二至第 N/2 个复数,代表着均匀频率间隔信号的特征。此复数的模,为此频率信号幅度的 N/2 倍;此复数的角度,为此频率信号的相位。一个奈奎斯特区包含 N/2 个频率点,频率点的间隔称为频率分辨率:
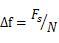
对上式稍作变换:频率分辨率的倒数,为可分析信号的周期:
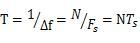
NT 即采样时间,可见 FFT 的频率分辨率,与其他参数无关,只与采样时间长度有关。
l 第 N/2+1 至第 N 个复数,从上文的奈奎斯特区可知,是 1st 奈奎斯特区的镜像,可以忽略。
3. 频谱泄漏与窗函数
在利用 FFT 对 ADC 的动态性能评估中,为了减少不相关因素对动态性能的影响,测试中一般要求给 ADC 低噪电源、低噪时钟,待测信号幅度尽量接近且略低于 ADC 的输入量程,而待测信号的频率 Fin 也有要求:
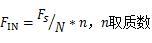
为啥频率要这样要求?将上式中的频率转换为周期就很好理解:
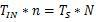
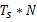 即为采样时间,采样时间刚好包含了 n 个整周期的待测信号。这样选取输入信号频率的原因,是 FFT 分析中默认采集到的数据,是原始连续波形中的一段周期波形。既然波形是连续的,那波形肯定首尾相连的、开始点电压值等于终点处电压值的。
即为采样时间,采样时间刚好包含了 n 个整周期的待测信号。这样选取输入信号频率的原因,是 FFT 分析中默认采集到的数据,是原始连续波形中的一段周期波形。既然波形是连续的,那波形肯定首尾相连的、开始点电压值等于终点处电压值的。
若采样到的数据不是连续的,则相当数据在首尾处有一个电压突变,电压突变在频域上就代表着很高的频率分量。这些高频的频率分量混叠到 1st 奈奎斯特区时,就会对原有信号的频谱造成干扰,这也叫频谱泄漏。
在实际的信号分析中,待测信号的频率是很难事先设定的,这就容易会造成频谱泄漏。为了减轻这个影响,FFT 加入了窗函数这个概念。窗函数,其实是一个加权系数,将不同位置的采样点,分别乘以不同的系数。经过加权相乘后,采样点就变成首尾相连的连续波形了。不同的窗函数,其加权曲线不一样,造成的影响就有所差异。举例 hann 窗的系数定义如下:
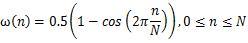
其 N=64 系数曲线与频谱如下:
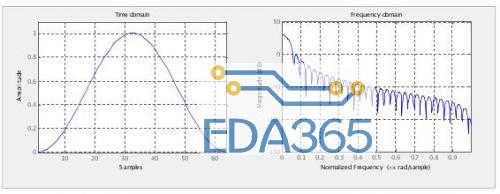
图 4 N=64 hann 窗系数曲线与频谱曲线
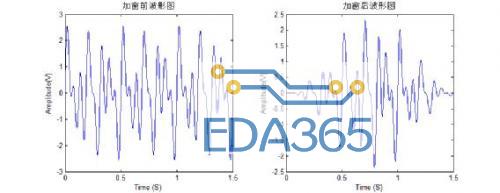
图 5 叠加窗前后的信号波形
4. 频谱图指标定义
将 FFT 得到的各个频率点幅度,绘制成随频率变化的曲线,可以得到信号的频谱图。在原厂 ADC 的器件手册或性能评估方案中,会有与性能相关指标的定义。在众多指标中,以下几个尤为重要:
l 信噪比 SNR
信号均方根幅值与除前六个谐波与直流分量之外的所有频率分量均方根和之比。在只考虑 ADC 的量化误差时,SNR 只与 ADC 的位数相关。
l 信纳比 SINAD
信号均方根振幅与出直流分量之外的所有频谱分量均方根和之比。SINAD 与 SNR 之间的差异只有前六个谐波分量所含的能量。
l 总谐波失真 THD
信号均方根与前六个谐波之和的均方根值之比。谐波的产生是因为信号经过了非线性环节,导致信号产生畸变。
l 无杂散动态范围 SFDR
信号均方根与最大杂散频谱分量均方根值之比。SFDR 可以表征信号分析的动态范围。
l 有效位数 ENOB
ENOB 反映了信号与正弦波的拟合程度。在 FFT 中可以使用公式计算:ENOB =(SINAD-1.76)/6.02。这公式是与基于 ADC 只有量化误差时的计算模型,具体的推论可以参考 ADI 的应用文档 MT-001《Taking the Mystery out of the Infamous Formula,"SNR = 6.02N + 1.76dB," and Why You Should Care》。
图 6 ZDS4054 Plus FFT 功能分析界面
ZDS4000 FFT 分析功能可以自动计算总谐波失真 THD、信噪比 SNR,显示前 10 次高功率信号频率。
FFT 是简便而高效的分析工具,在众多的软件中都已很好的集成。在网络上简单搜索一下例程,在 Matlab 软件中简单敲入 fft(),即可做信号分析。而 ZLG 立功科技 - 致远电子的高性能数据挖掘性示波器,FFT 分析的样本数可达 4Mpts,这使得示波器可以在最高采样率下,采样更长时间的波形。这样在 FFT 后,数据的奈奎斯特区就相当宽,而频率分辨率又相当窄,非常适用信号分析与噪声定位。


 APP下载
APP下载 登录
登录














 热门文章
热门文章