【导读】近年来,永磁同步电动机(PMSM)在电动车辆、电动飞机、机器人以及家用电器等工业制造中已经得到了越来越广泛的应用。而在永磁同步电机(PMSM)中,最常使用到的一项技术就是矢量控制,因为它可以实现更好的动态响应,充分发挥机器的潜力。
但若想实现矢量控制,就必须要确定转子的速度和位置。最常用的电机速度和位置测量传感器有光传感器和霍尔传感器。但这两种传感器都非常昂贵,会无形增加驱动系统的成本。
这里跟大家分享一种比较有前景的PMSM驱动解决方案,它将低成本的磁性角度传感器与动态观测器结合在一起,同样也能测量出精确的转子速度。本文为您展示的MPS电机控制模块就属于此类解决方案,模块包含了一个电机控制ASIC、一个磁性角度传感器、3相MOSFET功率级和PCB预驱动器,适用于NEMA 23和NEMA 17 两种型号的电机产品。
电机控制ASIC为电机驱动应用提供了极好的计算能力。该模块配合MA702(一款12位分辨率磁性角度传感器),可以检测出PMSM电机的绝对位置。MA702的成本要远低于光传感器和霍尔传感器。由于能够了解整个过程中转子的位置,所以可以通过建立基于PMSM机械方程的动态状态观测器来检测电机速度。ASIC可以使用动态观测器过滤掉位置测量所产的白噪音并估计出转子速度,从而在PMSM中使用磁场定向控制。
PMSM磁场定向控制
三相PMSM机械公式可以用方程组(1)表示:
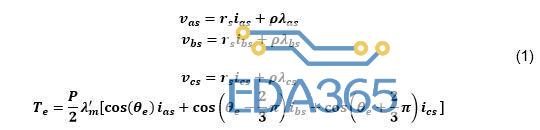
其中v、i和λ分别表示电压、电流和磁链。下标a、b和c表示相位a、b和c的变量。下标s为定子变量,ρ为特定值导数,P为PMSM的极数。
电磁转矩T_e由三相电流和转子磁链生成。λ_m^’为PMSM定子侧检测到的转子磁链。角度θ_e为转子磁链和A相定子之间的电磁角度。
为实现PMSM的FOC功能,需使用q-d下方的动态模型来解耦气隙磁链和电磁转矩。根据Clarke-Park变换计算公式,同步旋转q-d轴方程组(1)中的PMSM模型使用方程组(2)计算:

其中下标q-d为q-d轴变量。L_为自感系数,L_m为机械互感系数。为更加简化控制,转子磁链应与d-轴对齐,此时q-轴磁链则为零。磁链使用方程组(3)计算:

电磁转矩使用公式(4)计算:

根据方程组(1)、(2)、(3)和(4)的变换步骤,磁链可以直接由d轴电流控制。由于i_ds为常量,所以可以直接通过控制q轴电流来控制转矩T_e。如果保持i_ds=0,则电磁转矩直接与i_qs成正比。
由上述推导可以得到图1中的PMSM FOC原理图。
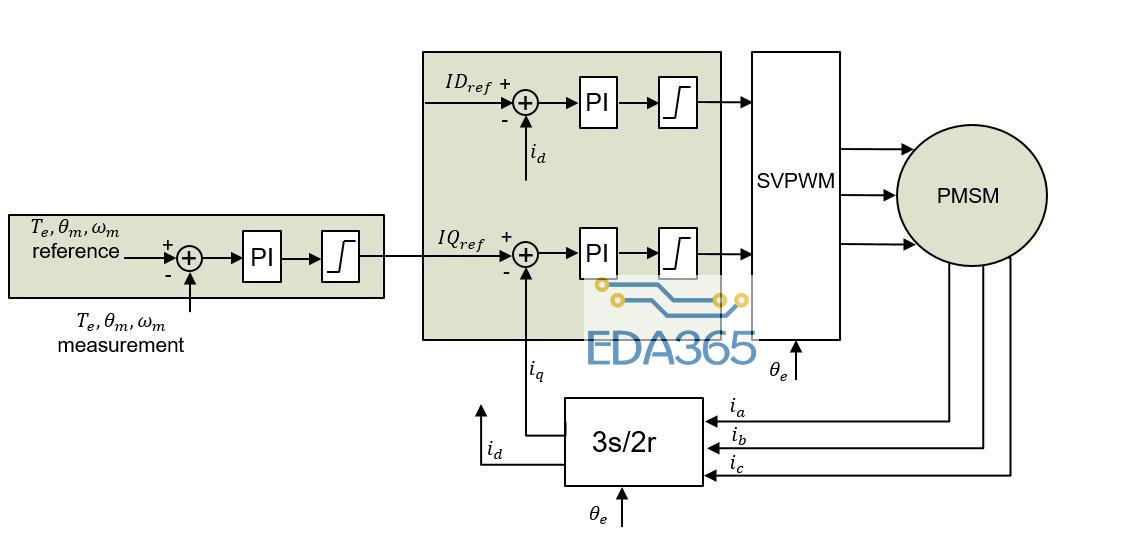
图 1:PMSM FOC 原理图
首先,对比外回路参考值与测量的反馈值,然后反馈输入差值至控制器(通常使用PI控制器),从而生成指令转矩电流IQ_ref。根据磁链要求设置d轴电流参考值ID_ref。电流调节器/控制器 VD_ref、VQ_ref、VD_ref和VQ_ref的输出值是空间矢量PWM(SVPWM)的输入值。SVPWM块为变换器生成栅极信号用来驱动PMSM。
基于无速度传感器驱动的动态观测器
MA702可以检测永磁体θ_e的位置。转子的速度可以通过公式ω_e=ρθ_e计算得出。作为一个数字传感器,MA702一定会在测量位置产生噪声。如果直接使用位置差分器获取电机的速度,则会破坏控制操作。解决这个问题最常见的方法是添加一个数字滤波器/观测器。
可以使用方程组(5)基于机械PMSM模型构建系统观测器:
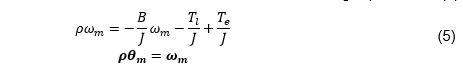
其中,T_e为电磁转矩,T_l为负载转矩。ω_m和θ_m为机械转子速度和位置,而ω_e和θ_e则为电动转子速度和位置。机械速度和位置乘以P/2等于电气速度和位置。P为PMSM的极数。参数J和B分别表示PMSM的惯性和以及转子与负载的组合粘性摩擦力。
MA702将绝对转子位置反馈到电机控制ASIC,使机械模型系统矩阵A成为一个简单的3x3矩阵,仅需两个非零元素。更简单的系统矩阵有助于减少MCU的计算负担,使算法更容易实现,执行速度更快。
使用欧拉(Euler)方法将方程组(5)中的PMSM力学模型离散化。状态变量x,∈和R ^ n作为系统过程的状态,离散时间可以用方程组(6)表示:
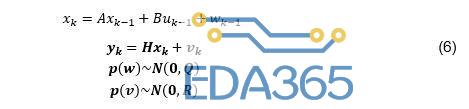
其中u是输入变量,y是输出测量值。w和v分别表示具有Q和R噪声方差的过程噪声和测量噪声。
根据经典控制理论,具有估计增益 K 的状态观测器可以用等式(7)计算:
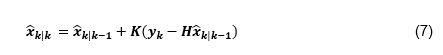
(∧) 表示了估计变量。与使用恒定增益 K 经典状态观测器不同,动态观测器在每次迭代时递归地更新其观测器增益 K 。
与FOC原理图(参见图1)相比,基于动态速度观测器的驱动器原理图使用机器测量作为系统输入来执行观测器(参见图2)。动态观测器输出滤波/估计的转子速度。转子位置用于传导PMSM的FOC。
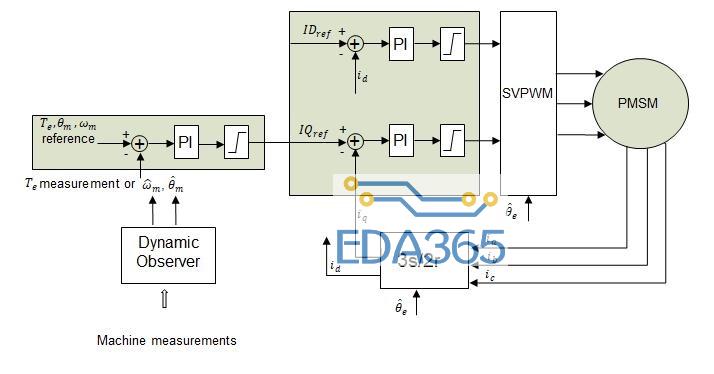
图 2:基于 PMSM FOC的动态观测器
仿真结果
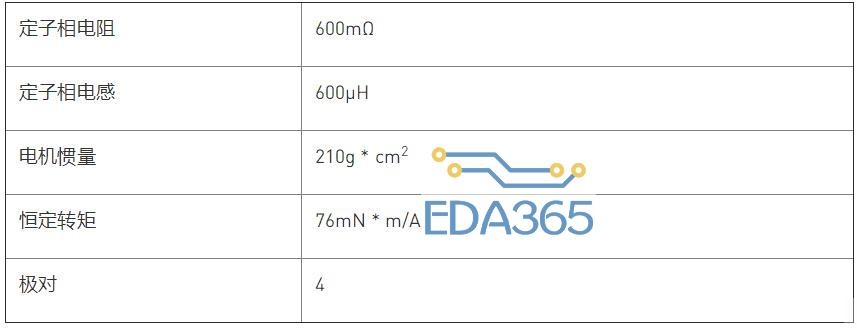
使用Matlab/Simulink得出仿真结果。用于验证算法的电机是MPS eMotion SystemTM智能电机MMP757094-36。MMP757094-36 是一款适用于伺服电机应用的全集成智能电机解决方案系列产品。表1列出了电机参数。
表 1: 电机参数
首先,将恒速参考值(500rpm)反馈至系统,以说明动态观测器在瞬态期间是如何工作的。
图3显示了估计速度如何跟踪实际电机速度。估计速度和实际速度在大约0.05s后都达到了稳定状态。图4示出了在速度响应稳定之后,误差方差矩阵行列式的绝对值下降到零。动态观测器增益随速度的响应而变化。在瞬态周期之后,观测器的增益K 变为恒定增益。

图 3:速度响应
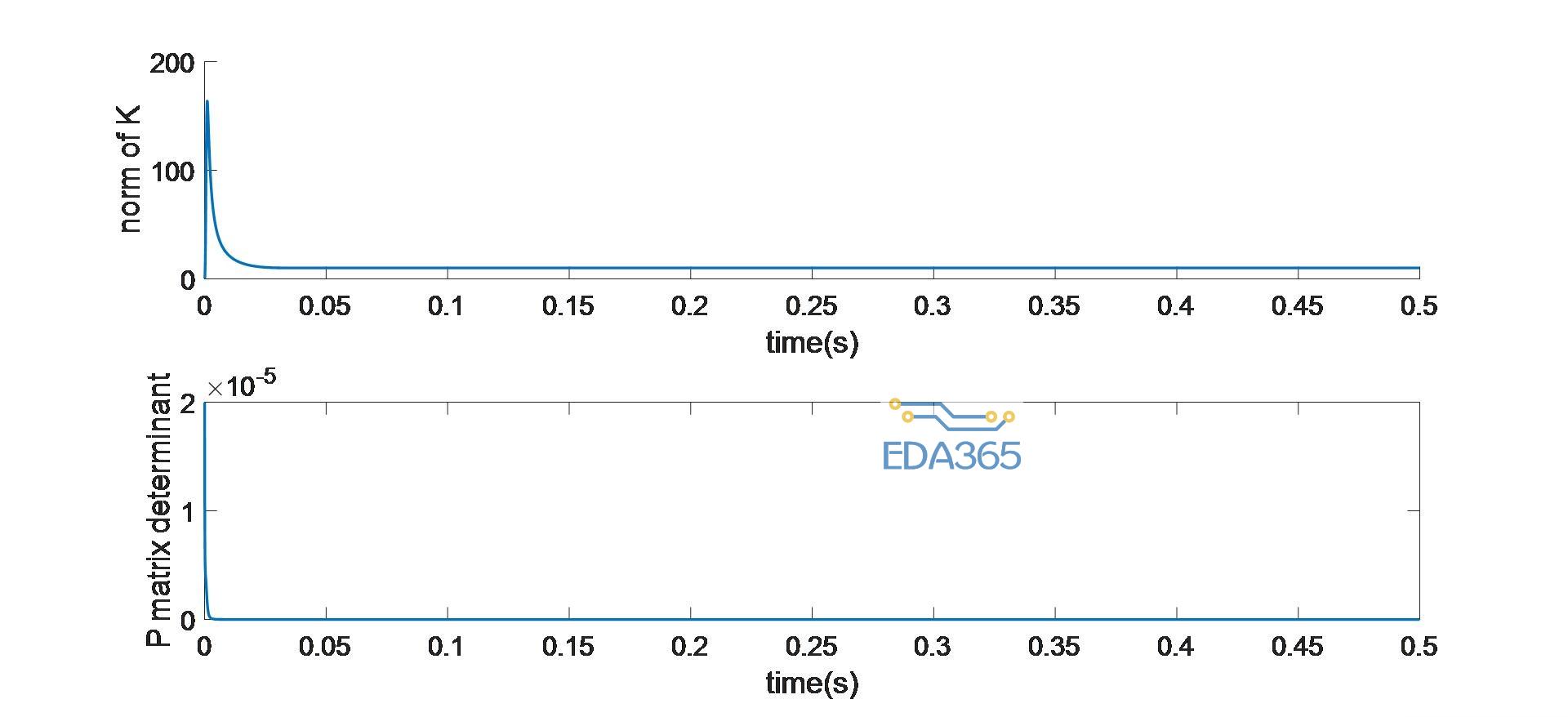
图4:误差方差和观测器增益动力学
实时硬件实验结果
为了验证算法,还测量了实时硬件实验结果。电机控制模块专为NEMA 23 57mm电机设计,可直接安装在电机上。

图5:MPS电机控制模块(左)和MPS智能电机(右)
如上一节所述,将MA702角度传感器采样的角度反馈到电机控制ASIC的绝对转子位置,使得动态观测器的递归迭代实现更加容易,并且减少了计算负担。由于测量只是一个变量,而不是经过复杂的矩阵变换,观测器增益计算变得更简单。每次迭代,整个动态观测器计算的时间不到20μs。

图6:实时的步进速度响应
图6显示了从1000rpm到-500rpm的各种速度参考值通过步进变化输入到仿真系统。动态观测器估计的速度仍然可以跟踪面对不同速度参考步骤的电动机速度。该算法还可以提供静止参考。
结论
本文为PMSM FOC提供了一种很有前景的解决方案,它将低成本的磁性角度传感器和动态观测器结合起来,以估算出准确的转子速度。该算法使用在MPS的电机控制ASIC中。MA702提供高分辨率的板上角度传感器,因此该算法避免了高维矩阵逆计算,这大大简化了代码开发和计算的时间。仿真和实时验证结果均表明所提出的解决方案具有良好的动态性能,并且能够在给定不同速度参考的情况下控制PMSM。

 APP下载
APP下载 登录
登录














 热门文章
热门文章