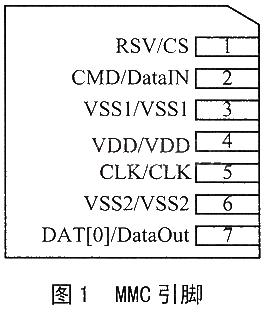
在设计运算放大器时,是不可能不含输入电容的,而运算放大器的印刷电路板上就包含更多了(图1)。除了反馈电容器CF,其他所有电容都是杂散电容,它们会影响电路的稳定性。 例如,如果人为将这些电容设置为零,则可以用公式1求得环路增益。运算放大器的开环增益a包含幅度和相位成分,因此波特(对数稳定性)图中会产生相移。波特图上的临界点是增益幅度等于零(增益=1)的点;180°与实际相移之间的差是相位裕量。
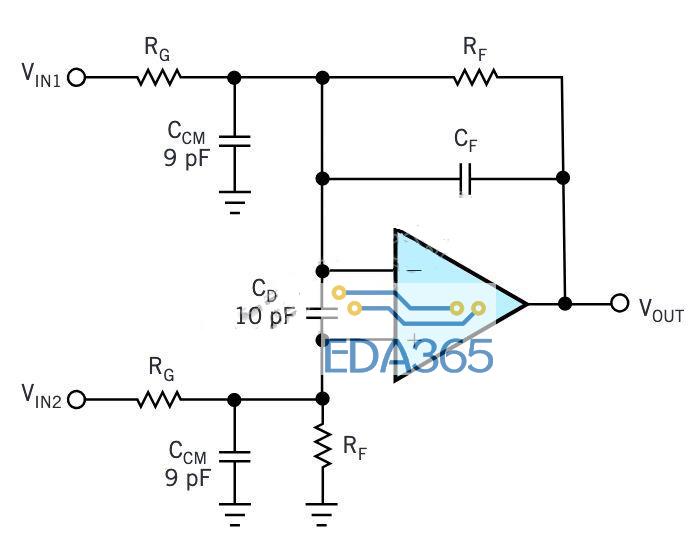

外部元件是电阻性的;令RG=RF,可以使环路增益降低6dB。这可以进一步增强稳定性,并使波特图上的纵截距下降6dB,而极点位置保持不变。公式2给出了具有实际输入电容(CF = 0)的反相放大器的环路增益,如图1所示。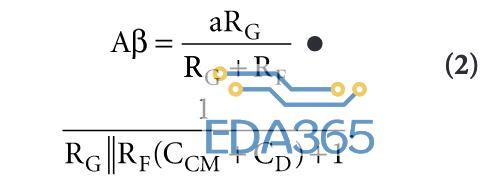
该输入电容向环路增益增加了一个极点,并且当RG和RF的并联值较小时,例如500Ω,极点位置位于f = 16.76 MHz处。该极点在其位置频率的十分之一处引起的相移基本为零,因此输入电容不会影响增益带宽小于1.676 MHz的运算放大器。当运算放大器的增益带宽超过1.676 MHz时,该极点引起的相移会增加至环路增益相移,并且运算放大器会产生过冲、振铃、随后振荡,这取决于其相位响应。
增加RG和RF的并联值会导致极点频率降低(RF || RG = 5kΩ时,f = 0.1676 MHz)。因此,相移发生得越快,不稳定性问题就越严重。传统的解决办法是,使高频运算放大器电路中的电阻较小,以最大程度地减小杂散输入电容的影响。解决输入电容问题的另一种方案是增加一个反馈电容CF。当电路中有输入和反馈电容时,由公式3可以计算出其环路增益。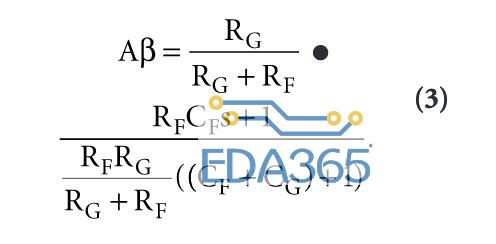
公式3中的零点始终先于极点; 因此,它的相移抵消了一部分负相移,直到极点起作用。通过使RFCF = RGCG,电路就可以独立于两个电容器。这种方法对闭环带宽性能而言通常并不是最佳选择,因此工程师选择使用较小的CF值。通过优化电阻值、电容值和运算放大器带宽可以获得最佳的高频性能,但在实验室,2CF = CG是一个极好的起点。
反相运放和同相运放的稳定性是一样的,因为稳定性与输入无关。反相运算放大器的工作很像理论预测,但是同相运算放大器的抗共模能力较低,因为一部分输入信号通过差分电容器(CD)馈入反相节点。抗共模性能的下降仅在高频时才明显。
『本文转载自网络,版权归原作者所有,如有侵权请联系删除』
 热门文章
更多
热门文章
更多