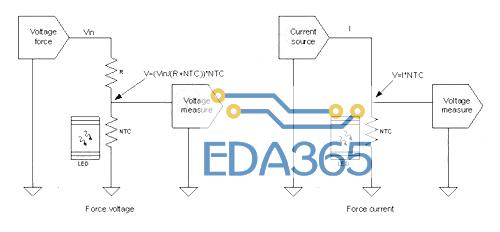
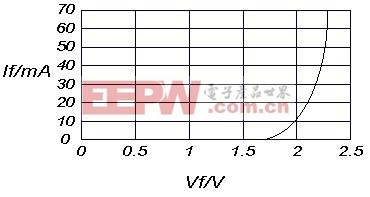
【导读】光模块采用基于雪崩光电二极管(APD)的光接收器支持高灵敏度设计。从 APD 接收到的反馈呈非线性(平均接收功率),这一非线性特性为优化控制激光器模块带来一定困难,典型的 APD 非线性特性如图 1 所示。
APD 特性
光模块采用基于雪崩光电二极管(APD)的光接收器支持高灵敏度设计。从 APD 接收到的反馈呈非线性(平均接收功率),这一非线性特性为优化控制激光器模块带来一定困难,典型的 APD 非线性特性如图 1 所示。
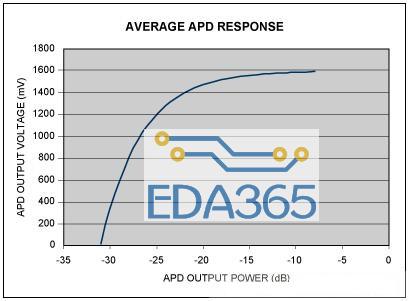
图 1. 典型的 APD 响应显示了非线性特性
为了保证精准操作,需要对 APD 的非线性进行补偿。补偿后可以为 SFP 控制器模块提供线性反馈,提高系统稳定性。补偿后的 APD 响应如图 2 所示。

图 2. 该平均曲线显示了所期望的典型响应,生产过程中对响应中微小变化的补偿是不可行的。
使用 RSSI 修正非线性
Maxim 的光控制器,如 DS1875,能够补偿 APD 的非线性。
DS1875 的一个输入通道(MON3)有两个工作区(细调和粗调)配置,每个区域都有其独立的量程和偏置,用于校准接收到的功率信号的非线性。校准通过对 APD 二极管的非线性响应进行分段线性近似,拟合完成。
除了提供两个独立的工作区,DS1875 也可在细调区域对 ADC 转换结果进行右移操作。即使输入信号不能完全覆盖输入范围,通过右移操作也可提高转换精度。
滞回的重要性
在给定的交叉点,DS1875 根据输入信号的幅度自动地在两个工作区之间切换。在交叉点提供滞回,当从粗调切换到细调时,切换点会发生变动。这能保证器件不会在两个工作区间来回触发,造成不稳定。
交叉点会根据针对细调范围的右移位设定的不同而改变,表 1 列出了不同的右移设置下交叉点的改变。需要注意的是,DEC 栏到滞回(hysteresis)栏对应的变化值。
表 1. 右移时的交叉点设置

校准 DS1875
DS1875 输入端 MON3 的两个工作区必须进行校准,这样才能准确拟合所要求的 APD 响应。按照下面过程进行校准,可以得到两个不同工作区的量程和偏置值。
对细调和粗调工作区进行配置,以保证每个工作区的实际响应为线性。写入工厂预设值,使响应为线性特性,同时将精调范围的右移位设为 3。
在 MON3P 接入两个输入("a" dB 和"b" dB)。使用内部工厂校准值,测量 MON3 转换数值。两个输入已配置成粗调范围使用"a" dB,细调范围使用"b" dB。输入可选择任何两个点,只要一个在细调区,另一个在粗调区。根据测试得到的误差,测量需进行再评估,直到得到最佳的分段线性拟合。
步骤 2 得到的数值与期望用来补偿 APD 非线性响应的数值会有差别。所有细调和粗调区的量程和偏置也需要校准,这样才能准确匹配期望值。
将两个被测值作为"x",这两个点的期望输出作为"y"值。
计算细调区 ADC 的量程和偏置。该计算使用两个点,第一个点为第一次计算中(步骤 2)的 b dB 输入测量的 x 值和 y 值(x1, y1);另一个点是(0, 0)点(x2, y2)。这个(0, 0)点是一个假设点,只需使用 2 个数据点即可得出量程和偏置。如果(0, 0)不适合所期望的响应,那么用户可以使用另一个数据点。
计算由下式完成:
y = m_fine × x + c_fine
其中,m_fine 代表量程,c_fine 代表偏置。
使用点(x2, y2),得到:
c_fine = 0
使用点(x1, y1),得到:
m_fine = y1/x1
为了得到所期望的响应,需找到最接近的右移位。将期望的输出(点 b dB 的 y 值)与表 1 的 DEC 值相比较。最接近上述期望输出的 DEC 值将被用作 x 值。与之相应的(y)值可以用上面的 m_fine 和 c_fine 推算,该点即为(x2, y2)。
使用(x2, y2)交叉点的值和 b dB 点(x3, y3)数值,由下式计算粗调区 ADC 的量程和偏置:
y = m_coarse × x + c_coarse
将偏置(c_fine 和 c_coarse)装载到 DS1875 相应的寄存器。注意,如果这个偏置为负值,那么将其 2 进制补码写入寄存器。
现在要分别整理细调和粗调区的量程,读出两个输入的期望值(a dB 和 b dB)。
基于修正过的响应(使用新的量程和偏置值)和期望的响应,可生成一条误差曲线(图 3 所示)。误差曲线根据两个点(a 和 b)的位置变化而变化。第一段斜线代表细调区的误差;第二段斜线代表粗调区的误差。误差大小可以根据客户要求,通过改变这两个点的位置进行调整。
结论
新的细调和粗调范围可用来检查器件是否近似拟合得到所期望的响应,图 3 为图 2 响应的拟合结果。

图 3. 这个误差曲线分别显示了使用新的量程和偏置进行修正的响应和所期望的响应
所期望的响应特性与计算得到的响应特性的误差如图 4 所示。
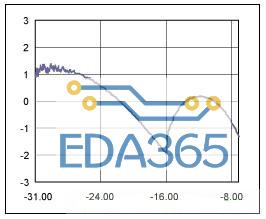
图 4. 计算得到的响应与所期望响应的误差


 APP下载
APP下载 登录
登录














 热门文章
热门文章