“二维思维”也叫结构化思维，顾名思义是将知识进行结构化的一种思维方式。

同样，在区块链系统中，不同的部分分别构成了不同的结构。

一般说来，区块链系统由数据层、网络层、共识层、激励层、合约层和应用层组成。

数据层封装了底层数据区块以及相关的数据加密和时间戳等基础数据和基本算法；

网络层则包括分布式组网机制、数据传播机制和数据验证机制等；

共识层主要封装网络节点的各类共识算法；

激励层将经济因素集成到区块链技术体系中来，主要包括经济激励的发行机制和分配机制等；

合约层主要封装各类脚本、算法和智能合约，是区块链可编程特性的基础；

应用层则封装了区块链的各种应用场景和案例。

区块链正是用这种方式使得本来繁杂的技术集合体变得统一高效。这种不同的层负责不同功能，使之结构化运行的思维正是我们今天要教大家如何使用的“二维思维”。

我们先假设一个场景，我们现在需要进行一次营销活动的策划，目的是为了销售公司产品。你会怎么去向老板介绍你的活动方案？

A：“嗯，我准备找两个歌星，让他们在我们这次的活动上唱歌吸引人气，顺便让他们拍一些宣传照，我们可以做为广告投放。再找一家人气够旺的商场办这次活动，那这样的话就要多请几个保安维持现场秩序。加上服装租用、灯光、音响、摄影，大概需要零时聘请十个人吧！”

B：“我制定了一份主题为****的活动方案，本次活动的目的是为了营销产品。所以我将本次活动规划分为：线上推广、线下活动两大部门，其中线上推广部门主要负责广告投放、电话营销，线下活动部门主要负责举办线下促销活动，线上线下结合将公司产品完整的呈现在用户的面前。”

如果你是老板，你会选择让谁负责这次营销活动的整体运营？

很明显，B的活动方案给人的感觉更有说服力，因为它将整个活动进行细分，不同的环节成立不同的部门，专人负责。而A的方案则给人感觉杂乱不堪，想到什么说什么，如果我是老板，我一定选择B作为本次活动的负责人。

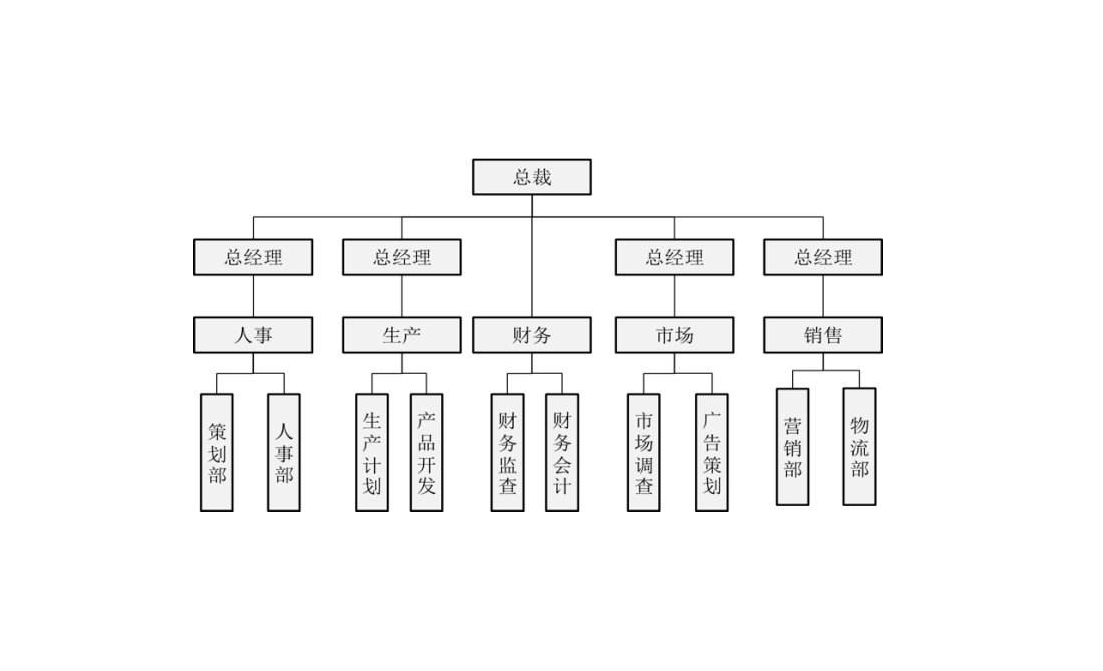
B的思维方式就是结构化的，他将本次活动中需要的大方向先设置为线上、线下，然后再根据线上线下的不同工作划分工作组。并且他的分类是符合MECE法则的。

MECE法则，即相互独立，完全穷尽。他把整体的活动方案定位线上线下两大块，这两块互相对立却又目的统一。在日常的工作安排中，以及公司的职能划分中我们同样要用到MECE原则，否则就会出现不同的部门负责的工作相互冲突的情况。

同样，如果现在你是人事部主管，公司需要招聘新员工，你会采取什么样的招聘策略？

这种情况我们可以用到四象限法。“四象限”法是美国的管理学家科维提出的一个时间管理的理论，同样适用于我们对工作的划分。

招聘新员工的一个重要指标就是能力，所以我们可以先把能力作为四象限的其中一个数轴，同时定义数轴的正方向为能力强，负方向为能力弱：

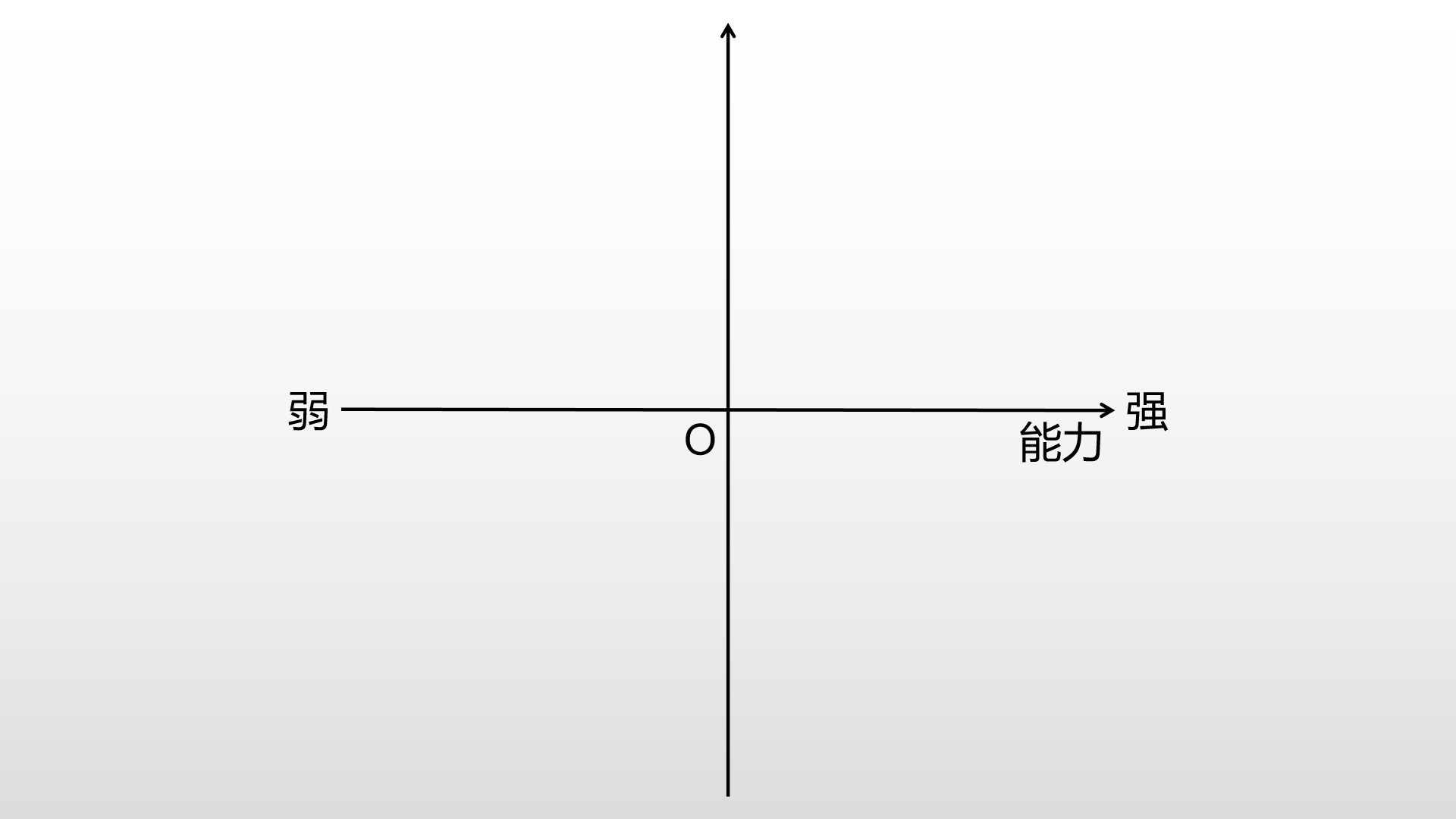
但是一个方向还不够，光有能力却无上进心的员工也不是企业想要的合格员工，于是我们有了选择员工的第二个方向—上进心，并且同样定义数轴的正方向为上进心强，负方向为上进心弱：

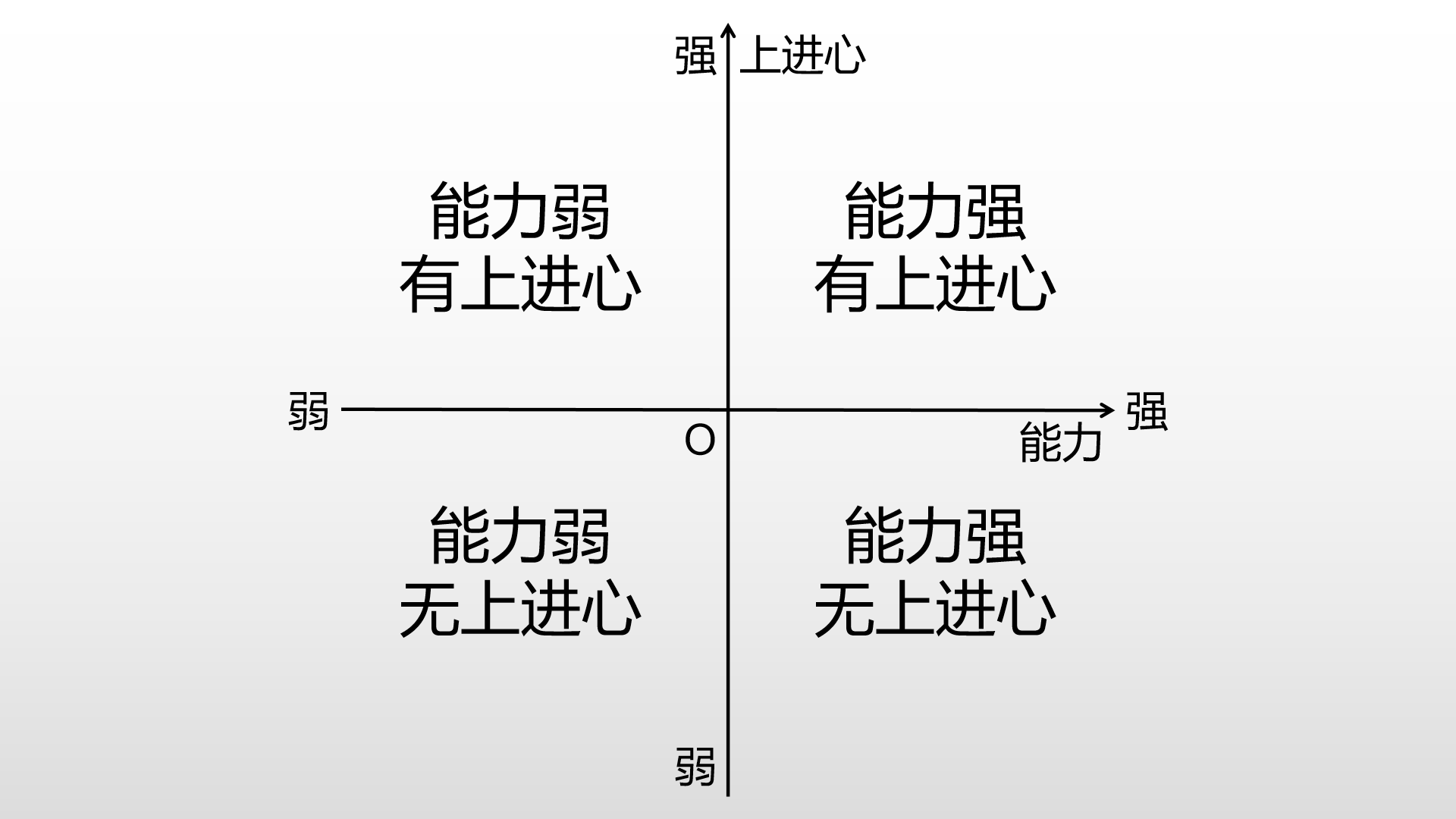
于是我们就得到了四种人员的分类，并且可以涵盖所有的应聘人员。这下我们就可以对这四种分类的应聘人员实行不同的招聘策略：

这种四象限法适用于简单情况下的情况以及对应策略分析，那如果碰到了复杂情况怎么办呢？

比如老板希望把应聘人员的服务态度作为考核的其中一个指标，又该如何呢？

如图，我们把服务态度作为额外的一条数轴，加入平面直角坐标系中：

然后重点来了，我们需要对三个要素进行单位长度的划分，其中，我们需要定义三要素的权重，以及考核标准。

例如：

定义工作能力的权重为40%，工作能力极差为0分，工作能力极强为10分；

定义上进心的权重为40%，无上进心为0分，上进心极强为10分；

定义服务态度的权重为20%，态度极差为0分，态度极好为10分。

根据以上的定义，我们就可以将三要素的单位画到我们的坐标系中了。

由于态度的权重只有20%，所以相同的分值，它在坐标系中表现出来的长度仅为其他两要素的一半。

假设此时来了三位求职者，面试官对他们三人的三要素打分分别为：

A：能力8分，上进心5分，态度5分；

B：能力5分，上进心6分，态度5分；

C：能力6分，上进心7分，态度10分。

我们在坐标系中对号入座，如图：

很明显，C在坐标轴中的三要素连接成的三角形面积最大。这表示他在三要素中的综合表现最佳，如果公司只能录取一个人，那他明显是三人中的最佳人选。

如果需要加入的要素更多，则可以用同样的方式增加更多的数轴，制定权重后画出面积，即可快速找到最适合的答案。

总结

“二维思维”即结构化思维，其目的在于将知识、思维、事务结构化，这样就能够更加快速准确的对目标进行分类，并找到合适的答案选项。

在运用“二维思维”的时候，我们可以用到“四象限法”。

在运用“四象限法”的时候我们需要注意两个细则：

1、MECE法则：分类应相互独立、完全穷尽；

2、权重：每个分类应当制定当对应的权重，有所侧重。

好了今天的《区块链思维》就到这了，喜欢我文章的朋友可以关注我的内容首发平台，同时你也可以在各大平台搜索“区块链方法论”以获得最新内容。

『本文转载自网络,版权归原作者所有,如有侵权请联系删除』