任何电子器件都会产生相位噪声，而振荡器是主要的噪声源。压控振荡器(VCO)在自激振荡或相位锁定时都会由于噪声调制产生相位噪声。这符合相位噪声指标表示频谱纯度的理论。例如一个理想的振荡器，输出是纯粹的正弦信号，在频域中是单一频点的垂直谱线。但实际上，振荡器所包含的噪声源会使输出频率偏离它的理想位置，在载波附近产生一些不需要的频率。

产生相位噪声的方法

有两种方法产生或提高相位噪声。一种方法是直接用噪声源调制振荡器或VCO。压控振荡器(图1a)利用锁相环(PLL)锁定相位，且环路滤波器的带宽比最小调制频率低。假如所考虑的最小相位噪声的频率偏差是10Hz (距离载波)，将锁相环的环路带宽设为1Hz。在压控振荡器的频率调谐输入端直接注入噪声，这样就会调制VCO在输出端产生相位噪声。此时，可以通过提高输入噪声密度增大相位噪声。

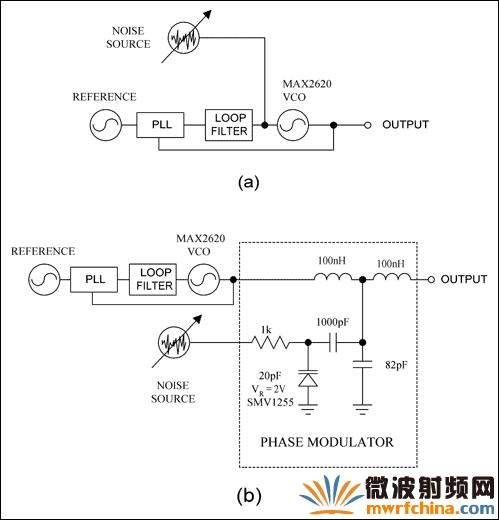
图1. 直接在VCO的调谐输入端注入电压噪声产生相位噪声(a)，或将噪声注入到相位调制器的变容二极管(b)。

输出相位噪声由VCO增益(KVCO)整形。假设VCO的频率是ƒo，在频率ƒn的1Hz带宽内被噪声源Vn(ƒn)调制。利用频率调制的窄带近似值¹可求得VCO输出：

第一项代表载波信号；第二项代表偏离载波处的噪声功率。相位噪声定义为频偏处的噪声功率与ƒo频点载波功率的比值。

Vn(ƒn)是在ƒn 1Hz带宽内的均方根噪声电压。相位噪声分布是噪声源分布除以ƒn。因此，用噪声密度分布平坦的白噪声(Vn(ƒn) = 常数)输入源调制VCO时，输出相位噪声分布每10倍频程降低20dB，如图2所示(假设调制产生的相位噪声远远大于VCO固有的相位噪声)。

图2. 直接在VCO的调谐输入端进行噪声调制所产生的相位噪声分布斜率为20dB/10倍频程。

产生相位噪声的第二种方法是用相位调制器在相位锁定的VCO输出端调制载波信号(图1b)。这种方法将噪声注入到相位调制器，也就是在LCL配置中的一个低通滤波器²。两个电感固定，电容通过变容二极管调节，可通过反向偏压将其设置为额定值。变容二极管的噪声电压会改变电容，从而改变相位。这样，噪声电压就会转化为相位噪声。增加噪声电压就会增加相位噪声。

这种相位调制方式对PLL环路带宽没有限制，所以为了获得更短的锁定时间，环路带宽可以尽可能宽。这种方法的另外一个优点是相位噪声分布与VCO增益无关，而由相位增益(KPHASE)决定，单位是弧度/伏。此外，相位增益由LCL滤波器的相位响应和变容二极管的电容特性决定。相位调制器的VCO输出是：

其中，Vn(t)是时刻t的噪声电压。相位噪声是KPHASEVn(t) = Φ(t)。可以通过对VOUT(t)做傅立叶变换计算相位噪声，但是很难求解。相位噪声的近似值³是：

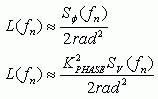
其中，SΦ是Φ(t)的谱密度，单位为rad²/Hz，Sv(ƒn)是Vn(t)的谱密度，单位是V²/Hz。因此，该相位噪声分布具有与调制噪声密度分布一样的波形。白噪声经过一个截止频率为100kHz的低通滤波器后，相位噪声分布同滤波器的频率响应相同。这种情况下，相位噪声在滤波器的截止频率内为常数，而在-3dB带宽外开始下降(图3)。使用相位调制电路可以很方便地产生可变相位噪声信号来模拟锁相振荡器等真实世界的噪声源。

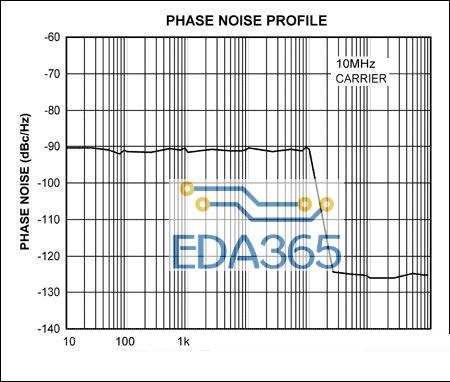
图3. 图1b的相位调制器所产生的相位噪声分布，相位噪声分布的波形与调制噪声密度分布相同，白噪声通过100kHz的低通滤波器。

图1b的电路可以在5MHz到30MHz的范围内正常工作，可以很容易地调整电感和电容值使其工作于其它频率。实验表明，该电路通过调整可以工作在高达2GHz或3GHz的频率下。这些频率需要大约1nH的电感和1pF的电容，所以这种方法受限于是否可以得到适当的元件以及PCB的寄生效应。

变容二极管电容的改变会同时改变噪声信号的幅度和相位。但是，幅度的变化比相位的变化小得多。相位的变化表现为相位噪声，而幅度的变化表现为幅度噪声(图4)。该调制器产生的相位调制比幅度调制大30dB，从而保证相位噪声起主导作用。

图4. 该图表示图1b在10MHz处的相位和幅度调制，相位调制比幅度调制大30dB。

产生噪声电压

可以通过许多途径产生噪声电压，用于相位噪声调制。最简单的方法是在齐纳二极管的雪崩击穿区域加反向偏压(图5a)。该二极管的多余散粒噪声经过固定增益放大器和可变增益放大器放大。这些级联放大器的增益必须足够高以产生期望的噪声电平。噪声输出将通过一个滤波器，该滤波器根据图1a或1b所示的相位噪声分布对输出噪声整形(图1b电路的一个优点是噪声源分布的形状和输出的相位噪声分布的形状相同)。

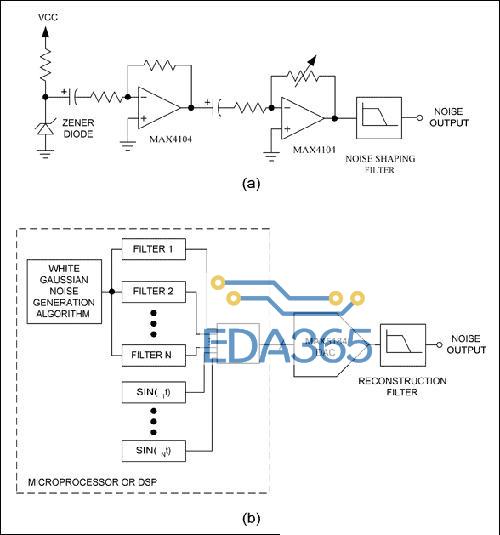
图5. 在齐纳二极管的雪崩击穿区域加反向偏压来产生白噪声。这个白噪声再经过放大、滤波产生用于相位噪声调制的分布噪声(a)。高级噪声发生器采用微处理器产生多段噪声分布，可以更真实地模拟相位噪声分布(b)。

实际振荡器的相位噪声分布可能很复杂，可能在低偏移频率时以30dB/10倍频程的斜率下降，在环路带宽内比较平坦，而在环路带宽外又以20dB/10倍频程的斜率下降，最终呈现为平坦的噪声底(图6)。这个相位噪声分布可能还含有一些杂散频率。

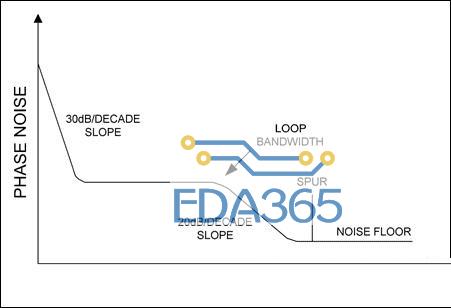
图6. 实际锁相振荡器的相位噪声在低频偏时以30dB/10倍频程的斜率迅速下降，在环路带宽内比较平坦，而在环路带宽外又以20dB/10倍频程的斜率下降，直到达到噪声底。还可能出现杂散频率。

这样的相位噪声分布需要更复杂的噪声发生器，如图5b所示。它利用一个微处理器或数字信号处理器(DSP)与一个DAC产生复杂的多段噪声分布。对于图1b所示的相位调制器，平坦的相位噪声区域由高斯白噪声通过一个数字滤波器产生，该滤波器在所考虑的频偏处具有平坦的频率响应(如带通滤波器)。为了产生所需的下降斜率，高斯白噪声需通过有限冲激响应(FIR)或无限冲激响应(IIR)数字滤波器进行滤波。寄生频率可以通过在噪声电压上加正弦波产生，然后把所有噪声段叠加起来。仍然是数字形式的噪声电压通过DAC转换成模拟电压，然后由一个重建滤波器输出。

结论

产生相位噪声的方法如图1所示，产生噪声电压的方法如图5所示。图1a中的电路通过直接调制VCO的调谐输入产生相位噪声，而图1b中的电路通过外部的相位调制器来产生相位噪声。每一种方法都可产生不同的相位噪声分布。图1a所示的直接调制法可以工作在任意的VCO频率。而图1b的相位调制法受限于是否可以得到适当的元件以及PCB的寄生效应，载波频率限定在几GHz。

参考文献
Behzad Razavi, RF Microelectronics. Upper Saddle River, NJ, 1998, pg 223.
Enrico Rubiola et. al., "The ±45° Correlation Interferometer as a Means to Measure Phase Noise of Parametric Origin," IEEE Transactions On Instrumentation and Measurement, Vol. 52, No. 1, pp. 182-188.
A. L. Lance et. al., "Phase Noise Measurement Systems," ISA Transactions, Vol. 21 No. 4, pp. 37-44.