前言

伴随着全球能源供应的环保化，风力发电作为一种清洁的可再生能源，有着取之不尽，用之不竭的优势，拥有非常广阔的市场前景^[1]。但风向、风速的随机性所带来的风力发电稳定性差是制约风力发电的瓶颈^[2]。为了克服这一技术难题，拥有智能、高效的风力发电变桨距恒功率控制系统显得极其重要^[3]。

由于风力发电系统是一个非线性、强藕合、多变量、大时滞的系统，难以实现准确建模。而人工神经网络技术不依赖于数学模型，可逼近任意非线性函数，具有较强的自适应、自学习和非线性映射能力，特别适应于复杂的风电变桨距控制系统建模^[4-5]。因此，本设计拟采用BP神经网络进行风电机组变桨建模。在该BP变桨模型基础上，利用MATLAB sumulink工具箱搭建风力发电变桨恒功率控制系统，并进行仿真验证。为了进一步验证本设计的合理性，将本BP变桨恒功率控制系统应用于山东长星风力发电机组，进行实验验证。

1 风力发电变桨恒功率控制系统

变桨距控制和恒功率控制是风力发电两大核心技术^[6-7]。在风速低于额定风速时，为了最大限度跟踪风速，此时没有必要变桨，只需调整叶片桨距角为规定的最小桨矩角，即β=0°，使其风能利用系数最大。当风速超过额定风速时，系统输出功率将会随着风速的增高而不断变大，这一过程对电网的稳定运行及设备安全有重要影响^[8-9]。因此，必须将输出功率限制在额定范围内。本设计将通过改变桨距角的大小，调整风能利用率，进而实现控制风轮转速和保证风电机组恒功率输出^[10-11]。

针对这一现象，本研究将主要针对额定风速以上的变桨恒功率控制系统进行建模仿真，其控制流程如图1所示。

为了保证发电机组向电网提供平稳电能，本风力发电变桨恒功率控制系统采用功率闭环控制方式。其中，变桨控制器利用BP神经网络建模实现。在此建模基础上，利用MATLAB sumulink工具箱搭建风力发电变桨恒功率控制系统模型，将发电机输出功率反馈到输入端与额定功率进行比较，其偏差值作用于变桨控制器，最终使发电机的输出功率稳定在额定值附近。

2 基于BP神经网络的变桨距控制模型

2.1 BP神经网络控制原理

BP神经网络是一种按误差逆传播算法训练的多层前馈网络，其结构简单、工作状态稳定、易于硬件实现，是目前应用广泛的神经网络模型之一。

BP网络能学习和存贮大量的输入-输出模式映射关系，而无需揭示描述这种映射关系的数学方程。通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。BP神经网络模型拓扑结构如图2所示。

BP神经网络通常由输入层(input)、输出层(output layer)和若干隐含层(hidden layer)构成。每层有若干个神经元组成，各神经元与下一层所有的神经元通过权连接，一个神经元可以处理多个输入信息。BP神经网络的自适应学习可归纳为 “信息正传播”→“误差逆传播”→“记忆训练”→“学习收敛”四个步骤。

信息正传播：外界信息经由输入层各神经元进入隐含层的神经元，并根据处理信息的复杂程度决定隐含层的层数，经隐含层和输出层各神经元逐层信息处理后向外输出信息结果。

误差逆传播：如果实际输出与预期目标存在差异，则将误差信息反向传送，不断记忆训练修整权值大小，最终达到期望值为止，从而实现神经网络的学习过程。

2.2 基于BP神经网络的变桨距建模

一个BP神经网络的建立通常包括网络层数、各层神经元个数、学习速率、初始权值和允许误差等参数。

1)BP模型网络层数和各层神经元个数的确定

BP网络一般包括1个输入层，1个或几个隐含层和1个输出层。虽然增加层数可以提高精度、降低误差，但这同时增加了网络的复杂性和训练时间。结合本研究实际，本建模将选用单隐层BP网络进行仿真。

通过分析影响风电机组输出功率的不同影响因素，最终确定输入向量分别为风速，风轮角速度，输出向量为变桨机构桨距角。利用试凑法，通过比较输出误差和收敛速度，最终确定隐层节点数为8。

2)传递函数的选择

该BP模型的网络的生成语句如下：

net=newff(minmax(pn),[8,1],{'tansig','purelin'},'trainlm')。其中，训练选用trainlm函数，隐层选用tansig传递函数，输出层选用purelin传递函数。

3)允许误差和初始权值的设置

本文允许误差设为0.005，初始权值选取(-1,1)之间的随机数。

4) 学习速率的选择

学习速率是优化计算中一个重要因子，反映网络一次循环训练中权值的变化量，取值范围通常在0.01-0.8之间。取值太小将导致训练时间过长，取值太大会导致系统不稳，因此本文中学习速率为0.05。

基于BP神经网络的变桨距控制模型结构，如图3所示。

BP神经网络变桨控制器模型建立之后，需要利用大量样本数据进行模型的学习训练。本文中的样本数据来源于山东长星风力发电实验室10kW风力机组的130组典型时段的样本数据，选取前104组数据用于网络训练，后26组数据用于网络的预测。

其中输入样本为各时段的风速、风轮角速度，输出样本为对应的桨距角。将训练样本数据做归一化处理后再输入神经网络模型中进行训练，得到网络的阈值和权值;把预测数据经归一化处理后，输入到训练好的神经网络中，就可以计算输出对应的桨距角值，如图4所示。

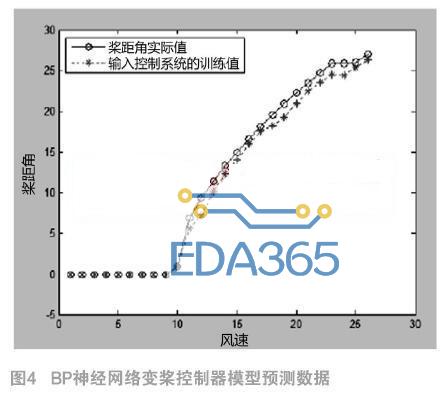
已知，该风电机组的额定风速为10.5m/s。从图4可知，随着风速的不断变化，该BP模型的桨距角预测值可以很好地跟踪实际值，预测效果较好。在额定风速以下时，桨距角为规定的最小桨矩角β=0°，可以最大限度地捕获风能。当风速超过额定风速时，桨距角不断增加，以期使风能利用率减小，从而将输出功率限制在额定值附近。

3 风电机组变桨距恒功率控制系统模型仿真

3.1 风电机组变桨距恒功率控制系统模型仿真

在已建好的BP神经网络变桨距模型的基础上，利用MATLAB仿真软件的SIMULINK工具箱搭建风电机组变桨距恒功率控制系统模型，结构如图5所示。

图6为60s的随机风速下，风电机组变桨距恒功率控制系统模型的输出功率情况。由图6可知，在60s的随机风速下，本文所设计的风电机组变桨距恒功率控制系统模型可以很快实现额定功率10kW的稳定输出，该系统具有很好的快速性和稳定性。

3.2 BP神经网络变桨距模型的实际测试结果

为进一步验证本变桨距恒功率控制系统在发电生产中的运行效果，将本模型嵌入至山东长星风力发电项目中，上机运行测试，测试结果如图7所示。

由图7(a)和图7(b)可知，在实际运行中桨距角随着风速的变化而随之自动调节。验证了BP神经网络变桨距控制系统发挥了控制作用。由图7(c)可知，机组的输出功率基本恒定于10kW，其上下波动属于合理控制范围内。图7说明BP神经网络变桨距控制系统，能够通过改变叶片攻角而达到机组功率输出恒定的目的，获得理想的控制效果。

综上所述，由于风电的强非线性，在不同风速下，桨距角的单位变化对发电机输出功率影响不同。为保证额定功率为10kW的稳定输出，在高风速段和额定风速附近，发生相同的风速变化△V，BP神经网络变桨距控制系统通过桨距角的不同调节可以很快实现额定功率的稳定输出。

4 结论

经仿真和实践运行验证，本文所设计的基于神经网络的风电机组变桨距恒功率控制系统模型控制效果良好，能根据风速测定值调节桨距角，实现在不同风速段对发电机输出功率的恒定控制，具有较好的稳定性和快速收敛性。