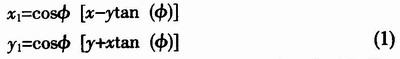目前的电子产品市场竞争非常激烈，厂商都希望能在最短时间内将新产品推出市场，以致子系统的设计周期越缩越短。在这个发展过程中，FPGA及ASIC的重要性越来越受到重视，例如新系统的很多重要功能往往需要由这些电路执行。对于采用FPGA芯片的系统来说，电源管理是尤其需要慎重考虑的关键问题之一。若要为FPGA芯片提供稳定的供电，我们需要全面审视系统的整体供电需要。这个取态也适用于特殊应用集成电路芯片。

由于系统的起始条件较为复杂，加上需要考虑的其他因素，例如瞬态行为、开关规格、以及许多其他的因素，因此电源供应系统必须符合一定的要求，这一点极为重要。若按照有关芯片的应用要求，供电干线必须绕过芯片或去除与芯片的耦合关系，那么处理旁路或去耦的问题时便需要特别小心。图1所示的是能够满足FPGA芯片供电需要的典型电源管理系统。一般来说，FPGA芯片最低限度需要两个电压为其提供供电。一个是专为“核心”提供供电的电压（1.0伏（V）至2.5伏［典型值］），而另一个是专为输入/输出提供供电的电压（3.3伏［典型值］）。许多FPGA芯片更另外需要第三个低噪音、低纹波的电压，以便为辅助电路提供供电。FPGA芯片所需的典型供电电压是2.5伏或3.3伏，但不同系列的FPGA芯片各有不同的电压需要。

异步降压稳压器

功能：降压（输出电压小于输入电压）

应用条件：一般来说，当输入电压是输出电压的3倍至5倍则输出电流介于0.5A至5A之间特色：若输入电压/输出电压/输出电流的典型值一如以上所提供的数值，设计这款电路便变得非常容易，而且有关设计更可发挥极高的效率

应用范围：所有降压稳压器及控制器同步降压稳压器

功能：降压（输出电压小于输入电压）

应用条件：当有高效率的系统要求输出较高的电流（5A以上），或占空比较低（输入电压比输出电压大5倍以上及/或输出电流不超过0.5A）特色：采用基本的降压稳压器电路布局，其特点是以第二个开关取代二极管，有助减少上述操作情况下的损耗应用范围：任何“同步整流”降压稳压器或控制器线性稳压器

功能：降压（输出电压小于输入电压）

应用条件：一般来说，有关应用的输出电流不能超过1A，压降与噪音也必须很低

特色：最适用于固定输出电压、低电流及低压降的系统，而且非常容易设计。

应用范围：任何低压降线性稳压器

建议：最适合微功率系统采用

操作时上述电路的每一电压并非输出恒定的电流，事实上电流大小取决于许多与实际应用有关的因素，例如FPGA芯片的速度及使用率等。操作电流可以低至100mA，也可高至20A。以这些系统来说，输入电压通常比FPGA芯片所获得的任何供电电压都要高，因此需要降低其电压并加以稳压。图2所示的是适合FPGA芯片采用的三款最常用的降压稳压器配置。这三款芯片分别是同步降压稳压器、异步降压稳压器及线性稳压器。为系统选用稳压器时，必须详细考虑系统的规格要求及稳压器的操作情况，以便作出配合。若要确保系统设计能顺利运作，我们也需要一并考虑以下的问题。

输入电压（VIN）FPGA芯片的供电全部由银盒、底板或中间供电干线提供。输入电压一般介于3伏至15伏之间，部分工业应用系统的输入电压甚至会高达30伏。输入电压可能不会为某一零件提供供电，因为稳压器的输入电压管脚已设定最高的额定供电量，只可为集成电路提供这一数量的供电。

输出电压（VOUT）及输出电流（IOUT）

稳压器的主要作用是稳定电压，换言之，无论输入电压及负载电流如何波动，稳压器都可将输出电压稳定在某一水平上。正如先前所说，操作电流可以在低至100mA与高至20A之间的范围内波动。输入电压、输出电压及输出电流等数值一经确定后，便可知道应该选用什么类型的稳压器。以下是可供工程师参考的一些前人的经验：

假如功耗不超过1W，应采用线性稳压器

”假如输入/输出电压比小于2:1，而输出电流不超过3A，应采用非同步降压稳压器

假如输入/输出电压比大于2:1，而输出电流又超过5A，应采用同步降压稳压器稳压器将参考电压与出现在反馈管脚上的极小部分输出电压加以比较，然后根据反馈的电压稳定输出电压。参考电压通常规定输出电压不能超过某一水平。

部分控制器规定启动时间不能超过某一时限。由于这个时限上的规定，稳压器无法调低太大量的输入电压。控制器的启动时间最低时限（TONmin.）也为输出电压设定限幅，限定某一频率下的输出电压不能超过某一水平。例如，启动时间若超过其最低的时限，输出电压便会升越规定的水平。

输入电压（VIN）=12V

输出电压（VOUT）=1.2V

1.2V

D=-------------=0.1

12V

示功耗的大小。但系统设计工程师很多时并不十分明白效率的真正意义。若输入电流无限制或电池寿命的长短不那么重要，功耗和效率也就不再成为最需关注的因素。系统耗散的热能会令系统元件受热，而温度的上升幅度与功耗的大小有直接的关系。受影响的元件包括集成电路、金属氧化半导体场效应晶体管（MOSFET）、电容器以及电感器。某一面积范围究竟会耗散多少功率？这一点也很重要。一般来说，1W的功率若通过一平方吋的铜质表面耗散掉，加上在没有气流的影响下，温度会因受热而上升40°C。

例如，假设：

输出电压（VOUT）=1.5V

输出电流（IOUT）=15A

效率=90%

功耗=2.5W

这一水平的功率若通过一平方吋的铜质面积耗散掉，会令温度上升100°C。

以下是另一可供参考的例子：

输出电压（VOUT）=1.5V

输出电流（IOUT）=1.5A

效率=81%

功耗=0.53W

若与前一例子中的90%效率比较，这个效率数字看来不大理想。但以这个例子来说，一平方吋面积所耗散的功耗只有0.53W，令温度只上升20°C，相比之下，前一例子的温度则上升100°C。以上例子证明功耗比效率显得更为重要。系统设计工程师若明白这个道理，便可为所设计的系统选择最理想的效率，以及降低系统的整体成本。体积系统设计所规定的芯片面积或高度如果缩小，不但会增加系统的成本，而且效率也会受到影响。例如，小型电感器的有效串联电阻（ESR）通常都比大型电感器高，而且体积小巧的电感器或小型电解电容器一般都较为昂贵。采用多层式电路板可以缩小体积，但一般来说会增加整体的成本。正如上文所说，部分系统设计工程师可能会刻意提高开关频率，以便缩小元件体积，但提高开关频率会增加功率损耗。若果没有必要而免强缩小电路板，不但会增加成本，而且会将功率损耗降低至不必要的低水平。

系统成本为FPGA芯片提供最具成本效益的供电一直是系统设计工程师的努力方向，但将供电成本尽量降低并不表示要采用最廉价的稳压器。例如，由于内置场效应晶体管的稳压器较为昂贵，因此系统设计工程师很多时不加思索便拒绝采用这类稳压器，但在某些应用情况下，这类稳压器比设有外置式金属氧化半导体场效应晶体管的稳压器更具成本效益。此外，设有外置式场效应晶体管的稳压器更易受来自电路板的噪音影响。设计简单而又内置金属氧化半导体场效应晶体管的高集成度开关稳压器便不易受噪音的影响，解决了大部分因为灵敏度过高而产生的噪音问题。此外，我们也应放弃采用双通道降压转换器取代两个单通道开关转换器这个念头。由于无需采用多个输入电容器，因此可以大幅节省成本，而且由于按照设计该两个相位可以异相操作，因此输入电容器的均方根（RMS）纹波电流可以大幅降低。采用双相位控制器可以避免拍频频率的出现，若采用多个非同步开关稳压器而它们都以稍微不同的频率操作，那就必定会产生拍频频率。我们不要忘记，真正的成本是系统物料清单上所开列的成本，并不是只计算个别元件的成本。采用FPGA的系统除了要符合这些规定之外，可能还要符合下列任何一项或多项的特别要求：瞬态响应FPGA芯片的核心电压会产生极高转换率的电流。为此，控制器必须一方面提供较大的阶梯级负载电流，而另一方面又必须将输出电压所承受的干扰减至最低。控制器因应这些负载作出响应的能力也因此称为瞬态响应。瞬态响应、输出电容及其有效串联电阻一旦确定后，会将操作带宽限定在某一范围之内。

排序及跟踪系统启动时，可能要先启动某一电源供应，然后才陆续启动其他的电源供应。若不按照规定的次序启动电源供应，电源供应便会“锁定”起来，而FPGA芯片可能会因此而受损或无法执行正常功能。部分FPGA芯片必须在输入/输出及核心电压之间设有排序及/或跟踪功能。（如欲了解多种不同的排序及跟踪系统设计方案，可参看图3。）若稳压器已设有供电正常（powergood）、允许（enable）、软启动及跟踪等功能，便可轻易添加排序及跟踪功能，或者以后可以随时添加这两个功能，令设计更具灵活性。若没有这两个功能，便需加设外接电路以确保可以按照正确次序启动电源供应。

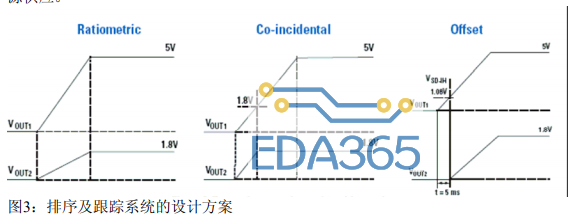
启动的要求我们若要为FPGA芯片设定电压上升率，可以利用软启动电容器加以设定。此外，启动时的上升电压一般都必须是单调的，而不是下降的。若电源供应的输出电容较小，启动时的电压会受其影响而下跌。容量够大的电容器可以储存足够的电荷，以便为FPGA芯片提供启动负载瞬态电压。同步操作同步操作功能的作用是确保两个或以上的稳压器可以一同锁定在某一频率，以免出现拍频频率。没有这个同步操作功能的系统都会出现拍频的现象。

总结

由于不同的系统有不同的要求，加上FPGA芯片或特殊应用集成电路各有程度不同的复杂设计，而且使用率也不尽相同，因此电源供应器的配置必须因应不同的要求而作出不同的安排。除了输入电压、输出电压及输出电流之外，我们也要考虑其他的特别要求如排序、跟踪及启动等条件。此外，我们设计系统时也需要顾及功耗、体积及成本对系统的影响。