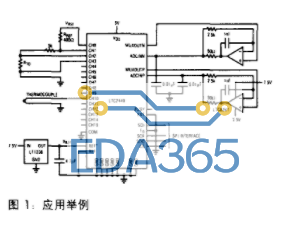
典型的信号采集链路会包含放大器，ADC 这些核心部件，根据实际的需求可能会有模拟开关一类的实现多路信号采样。通常放大器的噪声会有针对不同放大拓扑结构的计算方法，由噪声密度在等效带宽内积分而成，然后使用TINA-TI这种仿真工具实现噪声的仿真与验证。

通常在高精密系统里面，噪声是微弱的，比如下面的一个典型的放大电路，TINA-TI的仿真结果是噪声为300uVrms， 示波器对于这样的噪声测量是无能为力的。本文使用TI高性能的ADC的评估板， 像ADS127L01，结合Matlab的计算，来对放大器的噪声进行一个评估。

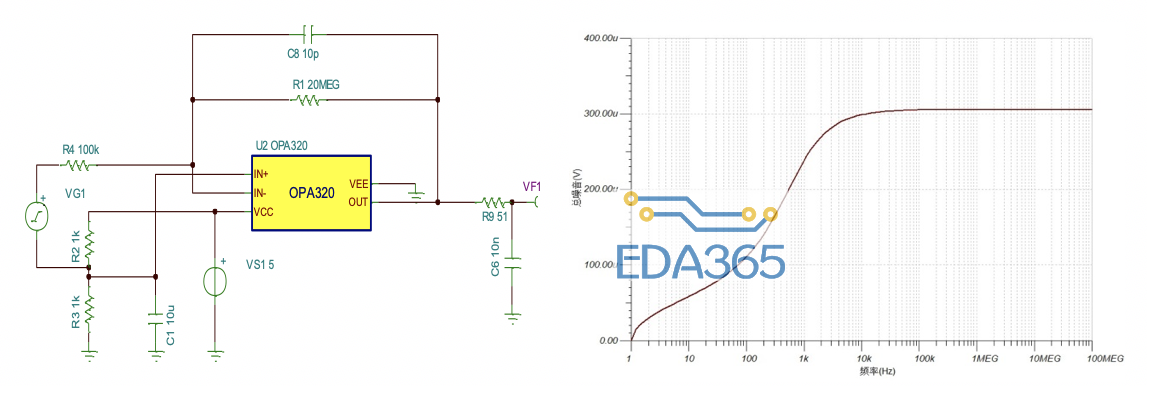
图（1）测试电路与仿真噪声

通过高精密的ADC去采集运放的输出噪声，可以利用几个表征ADC噪声性能的方法，STDEV，直方图和快速傅立叶变换。STDEV就是离散数据的噪声有效值，FFT通过累加各频率的分量，也可以计算出噪声的有效值，直方图用于观察样本的分布情况。

运放的噪声和ADC的噪声是相对独立的，可以通过噪声均方根的方式叠加。这样，就将运放噪声的有效值与评价ADC噪声性能的方法联系起来了。

由上式可以看出，要用ADC评价放大器的噪声，需要测量两组数据，一组是ADC本身的噪声，一组是连接上放大器的噪声。

我们用ADS127L01的评估板采集两组数据，然后分别使用matlab函数求解绘制STDEV， 直方图和执行快速傅立叶变换。下面来看一个具体使用到的matlab函数：

Avg = mean（num）; % 求解样本NUM中的平均值

Std = std（num）; % 求解样本NUM的STDEV，就是RMS值

hist（num，20）; % 将样本NUM的分布按照直方图绘出

y = fft（num，32768，1）; % 对样本NUM进行FFT

y1 = abs（y） / 16384; % 求解频谱分量的幅值

power = y1.^2 * 0.5; % 求解频谱分量的功率

TotalN = sqrt（***（power））; % 将噪声频谱累加

图2 为仅ADC噪声分析，左上角为ADS127L01评估板采样的原始样本，右下角为对样本做FFT后对各噪声分量的累加。

通过Matlab分析样本，得到样本的STDEV 为28.5uVrms。FFT分析做累加，得到了同样的结果，噪声有效值为28.5uV。

图（2）ADC噪声分析

图（3）为使用ADS127L01评估板采集图（1）所示电路的噪声分析，同样左上角为原始样本，右下角为对样本做FFT后对各噪声分量的累加。

通过Matlab分析样本，得到样本的STDEV 为263uVrms。FFT分析做累加，得到了同样的结果，噪声有效值为263uV。

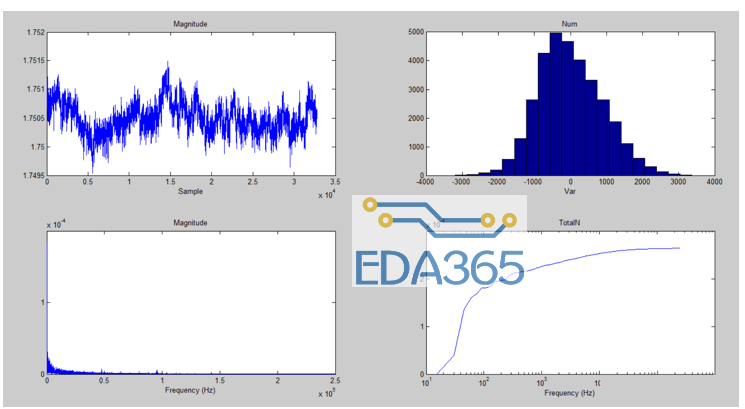
图（3）ADC+放大器噪声分析

根据噪声的叠加原理，图（1）所示放大电路实际测量噪声为261uVrms，仿真的结果为300uVrms。

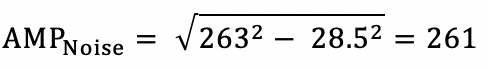
本文通过一个实际的例子演示了如何使用高精密ADC评估放大器的噪声性能，实验结果与仿真结果一致，并且提供了典型的matlab函数，利用STDEV， 直方图，FFT对ADC采集后的数据，对放大器进行噪声分析是一种直观且有效的方式。