遗传算法(Genetic Algorithm)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法,它最初是由美国Michigan大学J.Holland教授于1975年首先提出来的。随着经济社会的快速发展,人类科学研究与生产活动的广度与深度都大大拓展了。科研与生产实践中涌现出的大量新课题对作为社会发展催化剂的信息与控制科学提出了前所未有的挑战。传统信息处理算法在面对各种非线性、不确定、不能精确解析以及建模机理复杂的问题时,往往显得捉襟见肘。正是在这种背景下,各种智能信息处理算法如雨后春笋般涌现出来。作为智能信息处理算法中的重要一员,遗传算法近年来以其独特而卓越的性能日渐引起了人们的关注。
组合逻辑电路其特点是功能上无记忆,结构上无反馈,即电路在任意时刻的输出状态只取决于该时刻各输入状态的组合,而与电路的原状态无关。本文通过实例介绍组合逻辑电路的设计方法,并通过电子设计自动化EDA(Electronic Design Automation)进行仿真分析,使组合逻辑电路的设计变得更方便,更实用。
随着FPGA性能的不断提高,基于FPGA的计算加速已经逐渐成为提高计算速度和计算效率的重要手段之一。FPGA能够实现程序的并行化处理,不仅结构简单,而且有效地减少了运算时间、提高了运行效率,为遗传算法能在一些实时、高速的场合得到应用提供了依据。
1 基于FPGA遗传算法设计
遗传算法是一种多点并行的迭代搜索算法,它的每一代称为一个种群,由多个个体组成,每个个体称为染色体,染色体由一定数目的字符组成。每个字符称为一个基因,基因在染色体中的位置决定了基因所表达的特性。
文中基于FPGA的遗传算法,整个系统分为4个单元,4个单元分别为:选择单元、交叉单元、变异单元和适应度计算单元。
1.1 选择单元
选择单元执行遗传算法中的选择操作。选择策略决定哪些个体存活并得以繁殖,因其直接关系到遗传算法的运行导向问题故对遗传算法的性能有直接并且重大的影响。标准遗传算法所采用的***选择策略简便直观,但可能会产生较大的抽样误差。于是,各种改进的选择策略产生了。
最早提出的使用浓度控制的选择策略可以保证群体的多样性从而避免了早熟现象并且提高了算法的鲁棒性及运算效率。后来通过对浮点遗传算法早熟收敛现象的分析,有人提出了一种新的父代选择策略,即使用当前代的子代个体作为下代的父代个体,可使交叉算子持续地探索和开发新空间。目前,人们又发现可以通过选择策略的改变调控并维持种群多样性。这类研究成果中,文献中提到的重复串的适应度处理是一个有益的尝试。
1.2 交叉单元
交叉模块执行遗传算法中的交叉操作。由随机数模块产生的随机数与事先确定的交叉概率相比较,如果随机数小于交叉概率,则一对个体进行交叉操作,否则该对个体不变,直接进入变异模块。
文中一对个体进行交叉操作的基因位由随机数决定。随机数模块产生一个与个体等长的随机二进制串,若随机二进制串中的某一位为1,则该对个体中该位置的基因相互交叉;否则,该对个体中该位置的基因保持不变。
1.3 变异单元
变异模块执行遗传算法中的变异操作。与交叉模块相似,变异模块也是将随机数模块产生的随机数与事先确定的变异概率相比较,决定是否进行变异操作。同时个体中进行变异操作的基因位也是由一个与个体等长的随机二进制字符串决定的。对个体而言,执行变异操作的基因位不宜过多,否则容易对个体造成较大的破坏,影响种群的稳定性。本文将两个随机二进制字符串(每一位0、1等概率)进行相与操作,这样得到的新的随机二进制字符串中每一位为1的概率将降低到25%,用这个新的随机二进制串来决定个体变异的基因位。这样执行变异操作的个体中,每一位基因变异的概率也会降低到25%。
1.4 适应度计算单元
适应度计算模块执行遗传算法中的适应度计算比较操作,它根据适应度计算函数来计算种群中每一个个体的适应度,包括遗传算法开始时初始化产生的种群和后来遗传变异后产生的种群,并把每个个体的适应度大小保存到存储器中。同时,适应度计算模块还需要记录每一代种群中适应度最高的个体。适应度计算模块有一个内置的计数器,计数器随适应度计算模块的启动而启动,从0开始计数,每个时钟周期加1。计数器数值表示当前个体及其适应度在存储器模块当中的存放地址。适应度计算模块停止工作时,计数器会重新归零,等待新一轮的启动信号。
2 遗传算法的过程设计
遗传算法通过对当前种群施加选择、交叉、变异等一系列遗传操作,产生出新一代的种群,通过多次迭代,使种群逐步进化到包含或接近最优解的状态,如图1所示。一般来说,一个完整的遗传算法包括编码、初始种群的生成、用于进行个体评估的适应度函数的设计、遗传算子(选择、交叉和变异)以及控制参数(终止准则)的设定5个方面。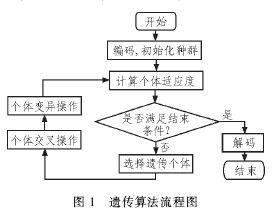
1)系统由外部给出reset信号:随机数模块开始产生随机数种子;控制模块重启,重新启动后,由该模块控制系统运行。
2)控制模块给出相应信号,初始化模块运行,初始化种群。
3)当初始化完毕后,有控制模块发出相应信号,系统进入进化计算阶段,进行遗传算法的具体操作。
4)各个遗传算法功能模块进行算子操作,经由交叉、变异、选择操作产生新的种群,同时记录系统的运行信息。如未完成本代进化计算,则重复本步骤。
5)完成一代计算后,由控制模块发出相应指令,存储相关运行参数、转换存储器的工作状态。如果以完成计算,则发出完成信号,如果未完成,重复步骤4)。
2.1 遗传算法编码
把一个问题的可行解从其解空间转化到遗传算法所能处理的搜索空间的转化方法叫做编码。编码方式应具有如下性质:完备性、封闭性、健全性和非冗余性。
遗传算法的编码方式有很多种,二进制编码方式是最常用的编码方式之一,最早由Holland提出。但是二进制编码的遗传算法进行数值优化时,存在连续到离散的映射误差、精度不高,最优解附近搜索较慢等缺点。虽然提高个体编码串长度可以提高精度,但是会使遗传算法的搜索空间增加,从而使得搜索变得异常缓慢。
本文中遗传算法主要解决的问题是组合逻辑电路的自动设计,组合逻辑电路由与门、或门、非门、同或门、异或门五种基本的门电路组成。在FPGA上进行遗传算法的编码,本文采用二进制字符串编码的方法,每个个体都有64位二进制数组成,由64位二进制数解码出一个组合逻辑电路。
2.2 随机数产生模块
随机数控制模块的作用是根据外部信号控制随机数内部模块,发出相应的使能、重启信号,产生随机数种子,从而产生随机数。
本系统中随机数模块所产生的随机序列由线性反馈移位寄存器(Linear Feedback Shift Registers,LFSR)生成。LFSR在FPGA上易于实现,且所产生的随机序列具有周期长、随机性好的特点。随机数模块需要向选择模块提供随机序列,作为存储器单元的地址,同时随机数模块还要向交叉模块和变异模块提供随机序列,用于确定是否执行交叉和变异操作,以及执行交叉和变异操作的位置。
2.3 存储器模块
存储器模块用来存储种群中的个体及其适应度。在本系统中,个体和适应度是分开存储的,因而对整个种群而言,其存储区可分为4个部分:父代个体存储区,父代适应度存储区,子代个体存储区以及子代适应度存储区。
由于本系统中的遗传算法采用完全流水线实现,因而必然会涉及到对存储器模块的同时读写操作,比如在选择模块从存储器模块中读取父代种群中的个体及其适应度的同时,适应度模块则在向存储器模块中写入子代种群中的新个体及其适应度。
3 实验结果
系统在Altera公司的Cyclone系列EPIC6Q240C8型号芯片上进行了实现。系统采用Verilog语言编写,开发平台为Altera公司自带的Quart usII 6.0集成环境。为验证系统的正确性和测试系统的性能,本文,对系统进行了测试,即给出一个三输入一输出的组合逻辑电路的真值表,测试真值表如表1所示。
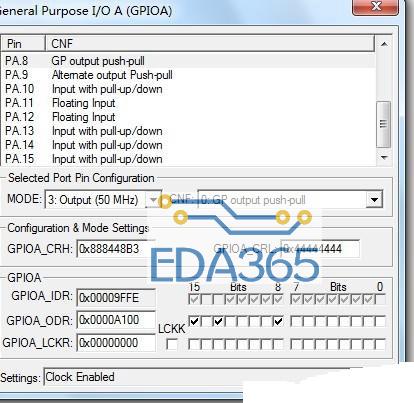
遗传算法参数设置如下:种群规模为100,交叉概率为0.6,变异概率为0.1,基因长度为16,遗传代数为100。其中针对给出的真值表,通过代码输入、编译、综合、布局布线后,得到结果如图2所示。
即最优解为:C3bFC396。经过解码,得到电路图如图3所示。所得到的电路图满足真值表的要求。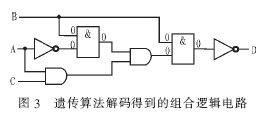
4 结束语
本文在FPGA上实现了基于遗传算法的组合逻辑电路的自动设计。对整个系统结构进行了自顶而下的设计,对模块功能进了划分。硬件实现遗传算法能有效地缩短运行时间,为实时应用提供了可能。随着FPGA芯片技术的进一步发展,大规模并行遗传算法的实现也将成为可能。


 APP下载
APP下载 登录
登录














 热门文章
热门文章