多采样率技术已广泛应用于很多领域。在一个信号处理系统中，在不同的地方使用不同的采样率有利于信号的存储、传输和处理。例如在数字通信中，网络的不同部分可能需要不同的编码格式，在这些编码格式的转化过程中，往往涉及到基本的采样率变换[1]。

FPGA是实现数字信号处理的一种高效手段。在实现高带宽信号处理领域，FPGA技术可以通过一个芯片上的多级运算单元来获得比通用DSP芯片更高的运算速度[2]。由于采样率变换能用一种并行的方法实现，使用FPGA来实现就可以利用其硬件本身的并行性得到较高的效率。

1 有理数采样率变换器的原理

从概念上讲，采样率变换器可以通过数/模转换，再对模拟信号进行给定频率的模/数转换得到。在实际的系统中，通过在数字域利用抽取和内插运算实现是一种更为合理和有效的手段。

抽取是降低采样率的方法。在时域上，D倍(D为抽取因子)抽取就是从原始序列中每隔D-1个样点取出一个构成新的数字序列。在频域上，这一运算可以看成是频谱的压缩, 即原来以Ω sat1为周期的频谱变为以Ω sat2为周期的频谱。为避免可能引起的混迭失真，抽取前应使原信号通过一个低通滤波器。其抽取的示意图及实现框图如图1所示。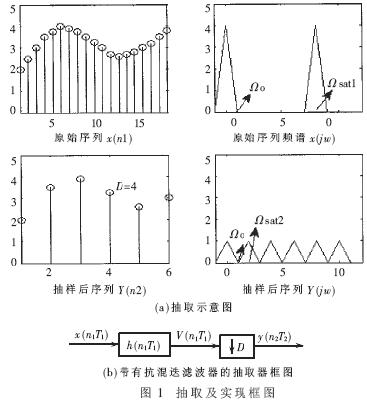

内插是提高采样率的方法。实际的内插系统由两部分构成：(1)零值插值器。设插值因子为I, I倍零值内插就是在原始序列任意两个样本间加入I-1个零值样本。在频域上，频谱进行了扩张,即原来以Ω sat1为周期的频谱变为以Ω sat2为周期的频谱。从Ω c到Ω sat2-Ω c的频带被称为镜像频谱。(2)低通滤波器。信号经过此滤波器后，镜像频谱被滤去，从而得到采样率提高的信号序列。内插图示及实现框图如图2所示。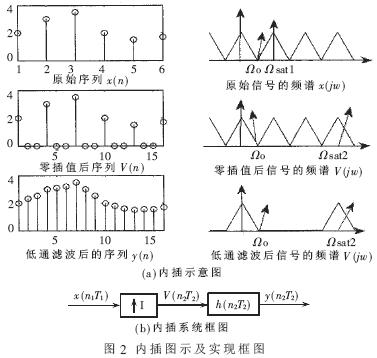

利用抽取系统和内插系统的级连，就可以得到有理数采样率转换器的基本方案。一般地，对于 I/D 倍数的有理数采样变换，通过先内插后抽取的方法，可以得到如图3所示的实现框图。图3(a)中的第二部分和第三部分是两个低通滤波器的级连，因而总的滤波效果等效为通带边缘较低的低通滤波器，合并后得到框图3(b)。

然而，对于上述三个系统，利用原始框图直接实现并不是一个很好的方案。如从图3可以看出，该系统最主要的运算量在滤波器的实现部分，图3(b)中滤波器的采样率为 F3=I，F1=DF2, 滤波运算是在最高采样率的部分实现的，这是不经济的。换一种说法，比如对后两级的系统，经滤波后的序列每D个样本中仅有一个是实际需要的，而D-1样本的运算被丢弃了。

2 FIR滤波器的多相分解与多采样率系统网络变换

利用FIR滤波器的多相分解[1～2]及多采样率系统网络结构的变换[1]，可以得到降低了运算代价的采样率变换器的多相结构。

FIR滤波器的多相分解是指将数字滤波器H(z)可分解为若干个不同的组。设H(z)的转移函数为：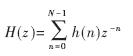

式中,N为滤波器长度，设N为D的整数倍, 即N/D=Q, Q为整数，可将冲激响应h(n)分成D个组，且有：

对于多采样率网络，存在下面几个等效变换:

T1: 抽取与乘常数可以换位。
T2: 零值插值和乘常数可以换位。
T3:两个信号先分别抽取然后相加，以及先相加然后抽取等效。
T4:抽样率相同的两个信号先分别零值内插(内插因子相等)然后相加，以及先相加然后零值内插等效。
T5：如果I和D 互质，则抽取与内插可以交换。

此外，Nobel关系式[3]给出了抽取/内插与滤波器级连时如图4所示的等效变换。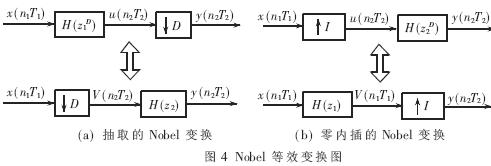

Nobel 关系式的意义在于：在抽取与滤波级连时，首先进行抽取运算，可以把滤波器的长度降低一个D因子; 内插与滤波级连时，首先进行滤波运算，可以使滤波器的的长度降低一个I因子。

3 采样率变换器的多相表示结构

通过对图1中的整数倍速抽取器系统进行多相分解(分解式1)，然后依次进行T3及Nobel变换(抽取)，可以得到抽取系统的多相结构。此结构中滤波器将在F2=F1/D的采样率下进行， 也就是说，对于给定的芯片和滤波器结构，滤波器能达到最高时钟频率相同时，该结构能处理的带宽是图1的D倍，或者说对相同采样率的数据，该结构对滤波器最高时钟频率的要求降低为原来的1/D，因而是一种高效的实现方式。

类似地，对图2中的整数内插系统进行多相分解(分解式2),并依次进行T4及Nobel变换(零内插),以得到整数内插的多相结构，通过变换，将以F1=F2/I的采样率进行滤波运算。

分数倍采样率转换器的多相结构有多种实现方案。

(1)如果I与D不互质,可以利用已经得到的多相结构，然后与抽取或内插级连实现。如图3(b)中可以把前两部分用图5的多相结构实现或把后两部分用图6的多相结构实现，具体选择时可参考D与I的数值。

(2)如果I与D互质,则可以转化为更为高效的多相结构[1,4]。图7即是I、D互质时的一种高效结构。这一结构的推导利用了多相分解的分解式1和分解式2、T1～T5以及两数互质时的欧几里德公式(若I、D互质，则存在整数p、q,使得pI+qD=1)。这样的结构不是唯一的，通过多采样率系统的网络变换，还可以得到其他的结构。在此结构中，滤波器运算是在F4的采样率中进行的，且有F4=F1/D=F2/I，与最初的形式相比，滤波器的最高时钟频率相同时，处理带宽增大为原来的I×D倍。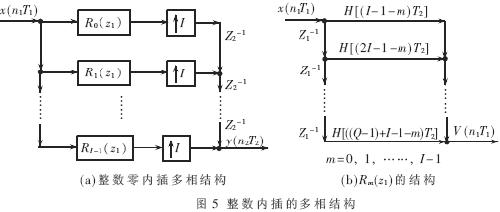





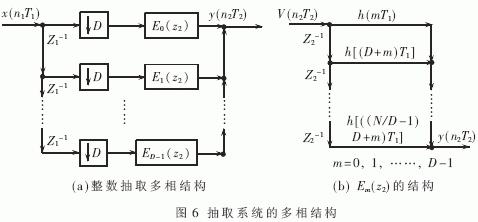
该多相结构中的Rm,n(z4)可以由原始滤波器经过两次多相分解而求得。特殊地，如果有滤波器的级数N=DI,则 Rm,n(z4)=h[(n+1)I-(m+1)T3]，为原始滤波器某一项的系数。

4 FPGA设计与验证

由于整数倍抽取和内插的实现过程可以包含在分数采样率变换器的实现过程中，因此下面只讨论I、D互质的有理数采样率变换器的实现。

根据图7的多相结构，对于I、D互质的分数抽样率转化系统，可以分解为四个模块：

(1)输入与延时链模块。这部分的时钟周期应该为T1。

(2)R0～RI-1的延时与抽取模块。注意：抽取器只是在第0,D,……,N×D个时钟周期让信号通过，其他时钟周期阻隔信号。若已知延时与抽取链的功能，则可用一个如图8(a)所示的多相选择开关来实现，而图8(b)给出了该电路的一种实现方案，其中TClk_T4 =DTclk_T1,T4为模块3的时钟周期。

(3)本系统最为关键的部分是第三部分。该部分是运算的主体部分，对整个系统的资源利用率和时钟性能有很大的影响。该模块需要实现的是I×D个FIR滤波器。对于给定的设计，这些滤波器的系数是常数,可由如下方法得到:

①根据低通滤波器的要求，用Matlab的FDAtool计算出滤波器的系数，并使其阶数N=M×I×D，M为正整数,可根据滤波器的需要选取。

②利用多相分解公式计算每个滤波器的系数。

③把所得到的数字进行定点化处理(比如系数同乘以2 048,取整，待计算出结果后右移11位)。
对于常系数的FIR滤波器，在FPGA实现时，有多种可以选择的方式以降低复杂性。在本设计中，采用简化的加法器图[3]来实现，避免了使用资源代价较大的通用乘法器，同时提高了系统的整体性能。例如，在测试系统的设计中，需要计算132×x(n)、28×x(n-1)、126×x(n-2)、13×x(n-3),用图9方案来实现时，将比用四个通用乘法器节省更多的LE资源，并且使最高的时钟频率得到了提高。表1给出了一个测试系统的资源与性能对比(使用了Altera公司的EP1C3T144C6芯片及Quartus II 5.1版本进行综合)。

(4)第四部分是与第二部分类似的模块。零内插器的特点是某个时钟周期有用信号通过，其余时钟周期通过零值，因而内插与延时相加模块也可用一个多相选择开关来实现。内插与延时相加模块实现电路图如图10所示。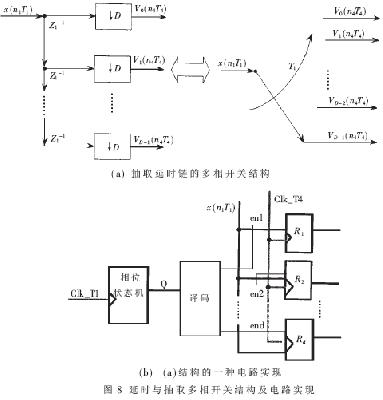






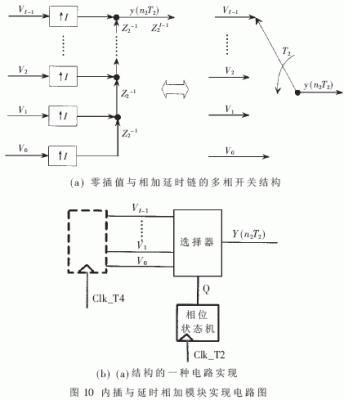
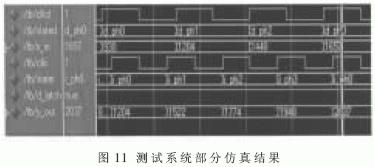
图11给出了一个D=3、I=4、N为12时的分数采样率变换的部分仿真结果(Modelsim 6.1)。其中，滤波器系数定点化为12位补码，输入、输出数据为12位补码整数, 测试输入序列为20kHz的正弦波波形序列，采样率为600kHz,输出为800kHz采样的正弦波序列。通过把输入输出序列保存并做FFT变换，可以得到两者的实际频率相同的结论。

利用FIR滤波器的多相分解及多采样率网络变换技术，本文介绍了一种有理数采样率变换器的高效多相结构，并结合FPGA芯片的结构进行了实现与优化。文中的一些方法也适用于其他多采速率系统的设计。