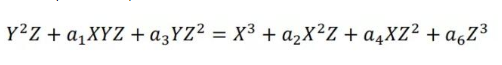共识算法作为区块链的基石之一，快速和不可逆是我们重点关注的目标。除此之外，为了更好地建设公链生态，我们认为公平性同样重要，如果大资本可以轻松占据公链中区块共识的话语权，那么会有很多公链上的开发者和用户的利益无端受损，一个不能保障公链建设者利益的生态，很难沉淀出价值深度，和星云链设计原则相违背。所以我们在设计共识算法时，在优先保证快速和不可逆的情况下，将尽可能追求公平性，维护公链建设者的利益。

常用共识算法的缺陷

我们试图在较为常用的共识算法中找到符合我们设计目标的选择，但是这些算法和我们的目标多少都有些差距。

PoW （Proof of Work） 工作量证明共识算法为零和博弈，采用竞争性哈希计算来确定记账人，导致了整个生态每次出块时都有大量电能在竞争中被无端消耗，挖矿成本高，而且速度受限。如果把公链参与者作为整体来看，随着参与挖矿的节点增加，每个节点获得记账权的概率将会减小，那么 PoW 协议下生态维持平稳出块的成本将会持续升高。不断增加挖矿难度的 Bitcoin 早晚需要⾯临矿机收益入不敷出的情形，而Ethereum 则早已在考虑使用新的 PoS 共识算法 Casper来逐步取代现阶段的 PoW 共识 。可见，从挖矿速度和经济成本⾓度，PoW 都不利于公链生态的长期快速发展，和我们“快速”的目标不相符。

PoS （Proof of Stake） 股权证明共识算法试图采用资产的多寡来取代算力的作用，按照币龄或者押金数额来分配获得记账权的概率，现阶段 Peercoin 和 Ethereum 的 Casper 协议都采用了 PoS 共识算法。这种算法解决了 PoW 高能耗的弊端，但很直观地放大了资本对记账权概率分配的影响，相较于 PoW，在PoS 下大资本更容易占据生态的话语权，形成大集团垄断，可能会对生态的建设者的利益造成损害，不利于公链生态的价值沉淀，同样和我们“公平性”的目标不相符。

PoI （Proof of Importance） 重要度证明共识算法最早由 Nem 提出，不同于 PoS，PoI 中引入了账户重要程度的概念，使用账户重要性评分来分配记账权的概率。这种算法解决了 PoW 的高能耗弊端，减缓了 PoS 的资本垄断危机，但暴露了 nothing-at-stake 的问题，作弊者逆转一个区块的成本被大大降低，和我们“不可逆”的目标不相符。

综上，鉴于常用共识算法和我们目标存在差距，我们提出了基于账户贡献度的 PoD （Proof of Devotion）算法，将评估账户综合影响力的 PoI 和具有严格经济惩罚的 PoS 相融合，利用 PoS 强化 PoI 的不可逆性，使用 PoI 反向遏制了 PoS 的垄断性，以此为生态自由快速发展助力。

PoD 算法设计

1. 新区块产生

类似 PoI 共识算法选取重要性高的账户，PoD 将选取生态中贡献度较高的账户，不同之处在于，PoD赋予选取出来的账户平等概率的记账权来参与产生新区块 （block），防⽌概率倾斜衍生垄断。

在选择贡献度较高的账户时，我们使用了星云链原生的 NR 普适价值尺度评估。在 NR 的算法设计中，着重考虑了账户的流动性和传播性，我们认为满足这些性质的账户对生态建设贡献度较高。所以在 PoD 中，将选取 NR 排名 Top N 的账户，这些账户自愿缴纳一定数量的 Nas 作为押金后则有资格成为新区块的验证者 （validator），参与记账。

在给定验证者集合 （validators set） 之后，PoD 算法通过伪随机数来决定验证者集合中谁是新的区块的提议者 （proposer），提议者产生新区块。验证者集合不是固定不变的，有资格的账户可以选择加入或者退出验证者集合，而随着周期性 NR 的变化，有资格的账户也会不一样。所以我们在 PoD 设计了验证者集合动态变化机制，来实现验证者集合的更迭。

2. 验证者集合更迭

验证者集合的更迭就如朝代变更一样，于是我们将验证者集合按照朝代 （dynasty） 做划分，一个朝代内验证者集合不会发生变化。一个朝代不能更迭地过快，至少要保持一段时间不做变更，因此我们将每 X 个区块定义为一个 Epoch，在同一个 Epoch 中朝代不会发生变化。所以朝代的变更只会发生在 Epoch 交接时，在此时将会考察上一个 Epoch 的第一个区块，如果此区块到达了 finality 状态，那么当前 Epoch 进入下一个朝代 D1，否则延续上一个朝代 D0 不变，如图13所示。

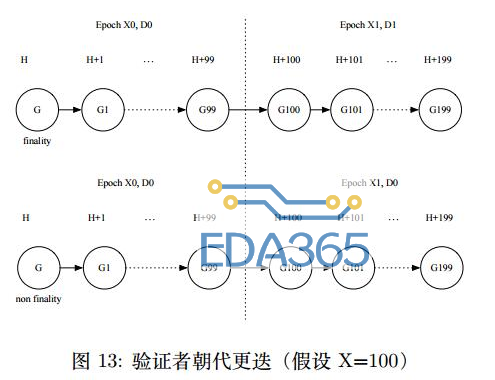
由于网络延迟，各个节点可能在朝代更迭时，看到的区块 G 是否 finality 的状态不一致，所以参考Casper 的动态验证集策略，要求每一个朝代的共识过程将由当前朝代和上一个朝代的验证者集合共同完成。因此在任意一个朝代，有资格的账户只能申请加入或者退出 D+2 朝代的验证者集合，当朝代变更到D+2 时，才可加入新区块的共识过程。

3. 共识过程

新的区块被提出后，当前朝代验证者集合中所有人将会参与一轮 BFT （Byzantine Fault Tolerant） ⽅式的投票，来确定此区块的合法性。在投票最开始，每一个参与此区块共识的验证者将会被从押金中收取 2x（x 为激励奖金⽐例） 的保证金，然后进入两阶段的投票过程。

• 第一阶段，所有验证者需要对新区块投 P repare 票，投完 P repare 票的验证者将获得 1.5x 的奖励，如果在当前朝代和上一个朝代中都有超过 2/3 的押金总额的验证者对新区块投了 P repare 票，那么该区块进入投票的第二阶段。此处需要说明，新区块的提议者将被默认对新区块投 P repare 票。

• 第二阶段，所有验证者需要对新区块投 Commit 票，投完 Commit 票的验证者，可以再获得 1.5x 的奖励，如果在当前朝代和上一个朝代中都有超过 2/3 的押金总额的验证者对新区块投了 Commit 票，那么该区块到达 finality 状态。

为了加速整个生态向前延展，如果区块 b 的 P repare 和 Commit 票的时间戳和区块 b 的时间戳相差超过 T，那么这些票将被视为过期，直接忽略。

4. 分叉选择

PoD 算法以每个高度上区块的得分来选择权威链，总是选择得分最高的区块加入权威链，在高度 h 的区块 b 的得分如下，

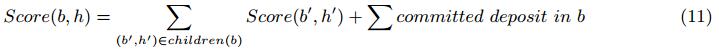
即为该区块及其所有后代区块收到的 commit 票对应的押金总和，如图14所示。

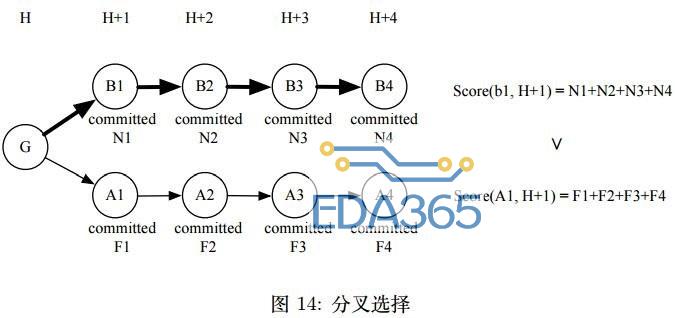
5. 投票规则

为了避免共识过程被恶意破坏，导致共识过程没法完成，阻碍生态发展，PoD 参考 Casper 的最小惩罚规则来约束验证者的共识活动。

假设共识过程中的 P repare 和 Commit 票结构如下，

• P repare（H， v， vs），其中 H 为当前区块 hash，v 表示当前区块高度，vs 表示 v 的某个祖先区块高度

• Commit（H， v），其中 H 为当前区块 hash，v 表示当前区块高度

PoD 算法为整个投票过程制定了如下 4 条基本规则，

• 单个区块的两阶段共识过程存在严格的先后顺序，只有在第一阶段 P repare（H， v， vs） 票总权值达到2/3 后，验证者们才可以投出第二阶段的 Commit（H， v） 票，

• 多区块间不强制一个区块共识结束后才能开始后一个区块的共识，允许交织共识 （interwoven consensus），但是不能完全没有秩序只有高度vs 完成了第一阶段过程，拥有 2/3 的 P repare（Hanc， vs， vs’）后，才可以基于 vs 对其后代区块投 P repare（H， v， vs） 票，保证交织稳步向前

• 为了避免有节点利用交织共识恶意跨多区块投票，要求基于高度 u 投出了 P repare（H， w， u） 票之后，对于高度在跨度 u 和 w 之间的所有区块，不能再投出 Commit（H， v） 票，保证共识过程的高效有序

• 为了制⽌节点用同一笔押金在多个分支上同时下注，导致 nothing at stake 的问题，要求在一个高度投出 P repare（H1， v， vs1） 票之后，不能再投出不一样的 P repare（H2， v， vs2） 票违反上述规则的验证者一旦被举报核实，将会被罚掉所有押金，举报者们将会共享罚金的 4% 作为奖励，罚金的剩余部分将会被销毁。

PoD 经济分析

1. 激励分析

参与 PoD 算法的验证者，在每一个合法区块上可以获得 1x 的星云币奖励，如果网络不畅或者有人作弊导致 Prepare 阶段没有办法完成进入 Commit 阶段，那么所有验证者将损失 0.5x。因此成为验证者的价值节点在保持网络畅通，不参与作弊的情况下，将共享大量记账收益。

2. 作弊分析

双重支付攻击 （double spend）

假设商户 merchant 等到新区块到达 finality 状态就确认交易发货，那么 fraud 要在 PoD 共识算法下完成双重支付攻击实现零成本购物要付出的最小代价如下：

⾸先，fraud 需要提高自己的 Nebulas Rank 到 Top N，然后缴一定数的 NaS 作为押金成为验证者，并申请参与 D+2 朝代区块的验证。

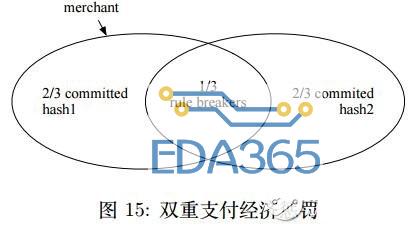
然后，fraud 需要被伪随机算法选中为新区块的提议者，此时 fraud 提出两个高度相同的新区块，一个哈希值为 hash1 包含 fraud 向 merchant 的转账交易，另一个哈希值为 hash2 包含 fraud 向 fraud 自己的转账交易。

最后，为了让 hash1 和 hash2 区块都到达 finality，如图15所示，fraud 至少需要花费所有押金的 1/3来贿赂 1/3 的验证者，让他们给两个区块都投 Commit 票。

所以要完成一次成功的双重支付攻击，fraud 需要花费一定的精力和财力来提升自己的 Nebulas Rank排名，然后等到幸运地被选为提议者时，至少花费总押金的 1/3 来让两个块同时到达finality 状态。

51% 攻击 （51% attack）

在 PoW 中要发起 51% 攻击需要 51% 的算力，在 PoS 中则需要 51% 的押金，而在 PoD 中，则需要验证者集合中 51% 的账户，这意味着拥有足够多的高声望用户进入 Nebulas Rank 的 Top N，并且需要支付对应的押金，因此在 PoD 中 51% 攻击将更为困难。

短程攻击 （short-range attack）

PoD 中的每个高度上的区块都有共识有效期，如果某个高度距离最新高度超过 100 时，该高度的所有区块在共识过程中将被视为过期，那么这些区块上的所有新的共识活动将会被直接忽略。因此要在 PoD 中完成长程攻击 （long-range attack） ⼏乎不可能，但是在有效期内依旧存在发起短程攻击的可能性。

短程攻击者 Attacker 试图在高度 H+1 的区块还没有过期的情况下，伪造 A 链来替代 B 链成为权威链，Attacker 需要让区块 A1 的得分⽐ B1 更高。由于多投会被严惩，所以 Attacker 将不可避免地要贿赂验证者，否则无法完成短程攻击。为了展现 PoD 共识算法的安全性，下⾯分别分析使不同数量的区块失效时，Attacker 需要付出的代价。

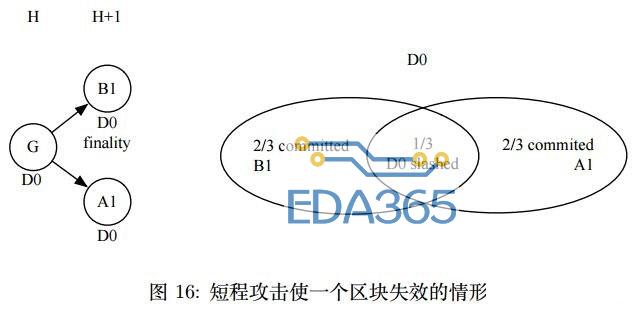
如果 Attacker 想要使 B1 失效，最小代价的情况如图16，就相当一次双重支付攻击，Attacker 幸运地成为了 H+1 高度的区块提议者，那么至少需要贿赂朝代 D0 中 1/3 的验证者多投使 A1 达到 finality，最小代价为所有押金的 1/3。

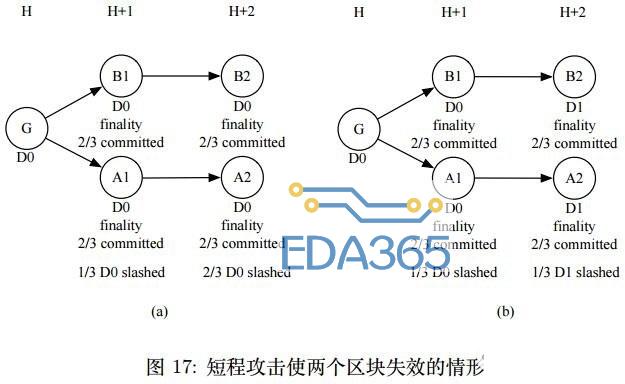
如果 Attacker 想要使 B1-B2 失效，假设 B1 和 B2 都已到达 finality，块中交易都已生效，为了让这些交易失效，这⾥考虑两种情况。第一种如图17中 （a） 所示，高度 H+1 和 H+2 在同一个 Epoch 中，朝代相同，那么 Attacker ⾸先需要贿赂 D0 中 1/3 的验证者使 A1 达到 finality，此时这 1/3 的验证者将会被惩罚，押金被罚完。在 A2 的验证中整体押金总和只有 A1 中的 2/3，此时 Attacker 想要让 A2 到达和 B2同价值的 committ 票，需要贿赂剩下所有没有作弊的验证者，合起来至少需要损失总押金的 3/3，即使如此也不能保证 A1 得分⽐ B1 高，攻击失败风险高。第二种情况如图17中 （b） 所示，高度 H+1 和 H+2 正好在不同的 Epoch 中，且朝代不相同，那么此时 Attacker 需要贿赂 D0 中的 1/3 来让 A1 到达 finality，然后贿赂 D1 中的 1/3 来让 A2 达到 finality，完成一次这样的攻击至少需要损失总押金的 2/3。综上，想要发起短程攻击导致两个 finality 区块失效，至少需要花费总押金 2/3 的代价。

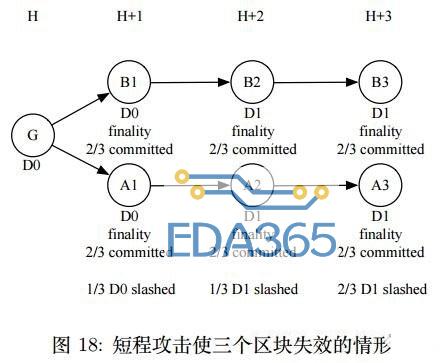
如果 Attacker 想要使 B1-B3 失效，如图18所示，Attacker ⾸先需要贿赂 D0 中 1/3 的人完成 A1 的finality，然后贿赂 D1 中 1/3 的人完成 A2 的 finality，最后需要贿赂 D1 中剩下 2/3 中的所有人来完成A3 的 finality，综上至少要损失总押金的 4/3。要完成这些攻击准备将会十分困难，而且即使有幸做到了，也不定能保证 A1 的得分⽐ B1 高，攻击也可能会失败。

如果 Attacker 想要使 B1-BN 失效，其中 N 受到区块共识有效期的限制，不会很大，由于 N = 3 时当前朝代所有验证者的押金就会被全部罚完，所以 N 》= 4 时，将没法完成攻击让 B1 得分⽐ A1 高，使B1-BN 失效，发起这样的攻击没有任何意义。

『本文转载自网络,版权归原作者所有,如有侵权请联系删除』