1 引言
    PMSM以其高效性、高转矩惯量比、高能量密度而受到诸多关注，因而在数控机床、军工、航天等领域逐渐得到广泛应用。交流步进传动控制是将位置控制、速度控制和伺服控制等不同的传动控制方式有机结合，使PMSM的气隙磁动势由连续的旋转磁场变为离散的步进磁场。对离散的步进磁动势进行控制，可获得良好的速度控制，还可进一步取得精确的位置控制，从而形成高性能的交流传动控制系统。电力电子技术的应用使系统具有离散控制的基本特征，使传统的运动控制思想得到突破。它打破了连续与离散、速度与位置、旋转与步进的严格界限，形成了一种统一的交流步进控制理论。

2 步进控制与矩角控制理论
2．1 步进控制理论
    PMSM的步进控制的中心思想是将电机的定子电流离散为bH步。每一步对应一个大小固定和位置步进的定子磁动势，与转子磁动势构成步进角，从而产生步进的复位转矩，进而将转子锁定在一个特定位置上。若将PMSM的定子磁势由旋转磁势离散为步进磁势，则定子气隙中所停靠的位置也就是该电机步进运动时能够提供的定位点数，即电机的每步数。当PMSM定子绕组输入三相对称正弦电流ia，ib，ic时，有：
   
    式中：Im为输入三相电流的峰值。
    将PMSM三相磁动势进行合成可知，三相绕组产生的气隙磁动势是一个旋转磁动势，其幅值是相脉振磁动势幅值Fa的1.5倍即。
    若按电角度计算，旋转磁动势在空间运行的电角度θ与绕组中电流在时间上经历的电角度永远相等，即：θ=ωt。当电流在时间上经历一个周期时，旋转磁动势在气隙中正好进行27π的电角度，故旋转磁动势每秒钟的转速为：n=f／pm。其中，f为定子电流的频率，pm为电动机的磁极对数。
    假设对于三相定子绕组，若不输入连续正弦电流，而是输入下列对称离散电流：
   
    式中：bH为环形分配器的循环拍数；k为主令脉冲的拍数。
    将输入电流的一个周期分为bH份(bH为正整数)，对于三相绕组，为了保证三相电流互差2π／3和各相的正负半周对称，最好取bH为6的整数倍，k为任意正整数。由此得到的气隙磁动势将是一个步进磁动势：。
2．2 矩角控制理论
    在PMSM的传动控制中，定子上产生的电枢磁势Fs与转子磁势Fr同步旋转，产生电磁转矩T。气隙中的合成磁势F=Fm+Fs。
    对于步进PMSM，需要特别关心Fs与Fr的夹角θ，即矩角。转矩方程为：T=CTFsFmsinθ。由于PMSM转子为永磁体，其Fr大小恒定，当Fs也为恒值时，T∝sinθ。PMSM矩角控制正是在此基础上提出的，即通过控制θ的大小，实现对T的控制。矩角特性如图1所示。

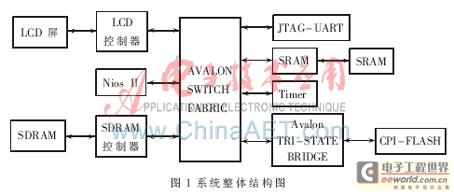
    图1以转子位置为参考坐标轴，定、转子的合成磁势定义为Fm=Fr+Fs。当θ=0时，Fm达到最大值；当θ=π时，Fm达到最小值；当0

[page]

2．3 定位控制方法
    一般的伺服控制系统将速度变化分为5段，即起动、稳速、降速、低速爬行及制动。当t=0时开始突跳过程。第1段0～t1为升频过程；第2段t1～t2为恒频过程；第3段t2～t3为降频过程；第4段t3～t4为爬行过程；第5段t4～t5为停车过程。五段速度定位示意图如图2所示。

3 仿真模型与实验平台搭建
3．1 仿真模型搭建
    该伺服系统的Matlab／Simulink仿真模型主要包括：电流滞环PWM逆变器模块、PMSM模块、Matlab功能函数模块等。工作原理为：通过电机测量模块获得电机转子的位置和速度参数，并将其反馈到Matlab功能函数模块，经过该模块和逆变模块将连续正弦电流离散化，形成步进电流。反馈部分通过测量电机的实际电流值与给定电流相比较，用电流滞环模块实现电机的自动控制，从而获得良好的动态特性和定位特性。
3．2 实验平台搭建
    全数字驱动控制器由DSP控制部分和驱动功率放大部分组成。控制部分的核心采用DSP芯片TMS320F2407A；功率放大部分的核心模块为智能功率模块IPMP型M15RSH120。控制系统硬件结构如图3所示。

    驱动控制器的主电路由整流电路、直流中间电路和逆变电路以及有关的辅助电路组成。主电路原理图如图4所示。此外，系统还设计了制动、过压及欠压等保护电路。

[page]

4 仿真与实验结果
4．1 仿真结果
    电动机在高速运行时，由于转动部分具有相当大的动能，起动和制动都需要一定的加速和减速时间。步进传动的突跳过程就需要一定的升速时间，在这段时间内，θ逐渐增大，转子转速逐渐升高，只要在转子转速升高到等于步进磁动势的平均转速时，电动机的动态角误差还没有达到允许的最大值，电动机就不会失步。
    在步进运动中，定子电流矢量的运行角度为θs，平均角频率为ω1，转子运行的角度为θr，角频率为ω，T与θ有关，而θ=θs-0r。只要能保证θ总小于允许的最大值，θs既可以恒定的角频率增加，也可以变化的角频率增加，前者ω1恒定，属于恒频控制；而后者ω1变化，属于升降频控制。升降频控制下速度、位置及转矩仿真曲线如图5所示。

4．2 实验结果
    为获得较大的起动、制动转矩，给电机输入不同的电流矢量。在第1，3阶段，输入两倍额定电流，使电机具有很大的加速度，在尽量短的时间内达到下一阶段，在其他阶段输入额定电流。
    第1阶段为升速过程，给定子超前转子3步的电流矢量并通以大的电流矢量，使电机以最大加速度加速，并在最短时间内达到恒定转速；第2阶段为恒转速运行阶段，将电机的速度控制在一恒定值。当转速低于设定转速时，给定子加超前的电流矢量；当速度高于设定转速时，给定子加滞后的电流矢量，这样就能尽量使电机速度控制在恒定转速；第3阶段为减速阶段，电机定子的给定电流滞后3步转子的电流矢量，这样电机以最大加速度进行降速，当电机运行到设定的脉冲数后，电机将进入低速运行阶段；第4阶段为低速运行阶段。此阶段运行速度较低，主要作用是为了减小电机惯性，实现电机最后一个阶段的精确定位；第5阶段为制动定位阶段，当电机转速趋近于零时，为保证定位的精确，令定子磁动势的位置保持在设定的目标位置上，此时产生复位转矩Tx，Tx将力图迫使转子回到提前设定的位置上，从而实现电机的定位控制。五段速度实验曲线如图6所示。

5 结论
    通过对矩角控制下PMSM伺服控制系统的仿真和实验可知，运用矩角控制理论的PMSM伺服系统具有良好的动态特性与定位特性，完全可以
满足现实中对于速度以及定位精度的高要求，同时对于PMSM在高性能控制场合下的应用打下坚实的理论与实验基础。