摘要
环路控制是开关电源设计的一个重要部分。然而，由于各种原因，在选定主要元件后，研究往往在项目结束时被抛到了脑后。通过简单的试验和错误分析，我们有时候会觉得，如果设计能够在示波器上实现可接受的瞬态响应，那么该设计便已准备好用于生产，但这种想法非常不明智，而且可能导致高昂代价。这是因为，转换器中使用的大多数元件都会受到杂散元件的影响，而杂散元件的广泛影响在原型制作阶段是隐藏的。如果未在模拟和环路测量的基础上进行彻底分析，您就不会知道相位和增益裕度是什么样的，以及它们有多可靠。这种设计松散的转换器很可能在生产中或在现场上电后不久就会出现故障。为避免出现这种情况，本文综述了目前可供选择的一些工具，让您在开始生产之前能够计算、模拟和测量您的原型，从而确保生产工作安全顺利。

I. 简介
在开关转换器中，功率级的输出由电压变量控制。本文将这类电压变量记为 Verr 或 Vc，它们由负责将转换器输出维持在规定范围内的补偿模块提供。对于以固定开关频率 Fsw 运行的转换器，控制变量为占空比 D。但情况并非总是如此，有些转换器由可变频率（例如 LLC 等谐振转换器）或者可变导通或关断时间控制。本文将主要讨论以固定开关频率运行的转换器类型。

误差电压 Verr 可以直接控制占空比，我们这里讨论的是电压模式控制(VM)或直接占空比控制。另一方面，在电流模式控制(CM)中，控制电压 Vc 通过感应电阻按周期固定电感峰值电流，并间接设置工作占空比。然而，当使用示波器显示在 VM 或 CM 下运行的转换器波形时，您无法判断转换器是在电流模式控制还是电压模式控制下运行。这是因为这两种结构的功率级非常相似，只有详细阐述占空比的方式发生了改变：降压转换器采用 10V 电源为负载提供 5V 电压时，无论该系统在电压模式控制还是在电流模式控制下运行，该转换器在理论上都将具有 50%占空比。

作为电源设计人员，我们的目标是构建出稳定的转换器，既能够提供精确调节的电压（或电流），而又对工作条件（输入源变化、环境温度变化、不同负载条件等）不敏感。除了这些实践要求，设计人员还必须确保其转换器在整个使用寿命期间都能保持稳定和正常运行。您还必须考虑到自然生产误差或因老化而导致的元件性能下降。现在还不错的裕度在 5 年后会变得如何？如果我的买家朋友向我展示工厂选择的更实惠的新型电容，我对自己的选择有多大信心？“嗨，Anaximander，如果输出电容选择 B 品牌而不是当前储存的 A 品牌，您能确认新一批 100 万件适配器会工作正常吗？”您能大胆地回答这个问题吗？如果您做足了功课，并仔细研究了寄生电容对交越频率和相位裕度等的影响，那么您确实可以。但是如果您没有那样做，而只是在实验室内转动补偿器的 R 和 C 旋钮来观察了阶跃响应，那么您可以擦擦额头上的汗珠，未来几天您肯定都要加班到很晚来纠正错误，避免出现灾难性结果。

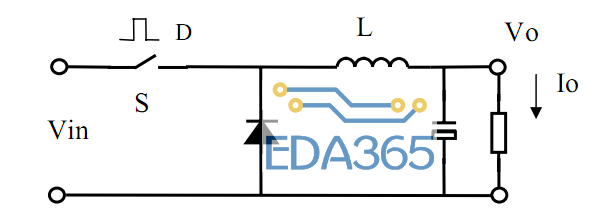
要避免这种困境，一种方法就是按章办事，并从功率级响应开始。这是唯一的起点：在考虑可能的控制策略之前，您需要先表征您要控制的系统。您需要的是确定输出变量对控制输入的变化有何响应。换言之，您需要待构建降压或升压转换器的控制到输出传递函数：Vout 会对 Verr 中的指定激励做出怎样的动态响应（图 1）。也就是说，设备会做出什么响应？

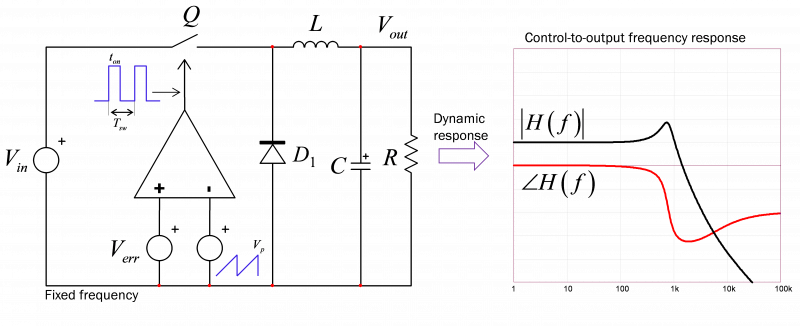
图 1: 我们想要功率级动态响应。

拿到传递函数幅相图后，您就可以考虑补偿策略（即在不同的频率位置放置极点、零点和增益（或衰减））来满足您的设计目标。这就是图 2 中所示的示例。D1

构建补偿器时，有几种方法可循，如图 3 所示。经典方法在文献中存在大量描述，该方法采用运算放大器构建滤波器，因为补偿器就是一个有源滤波器。然而，业内主要采用 TL431，您可以在当今市场上销售的绝大多数适配器中发现其痕迹。我承认，就简单性或成本而言，它是其他方法无法超越的：只需几美分就可以得到一个具有适度高开环增益(55 dB)和 2.5 V 精确基准电压的运算放大器，而且 TLV 版本的 Vref 低至 1.24 V。该部件提供多种不同的封装，一些版本可以接受高达 36 V 的电压。然而，选择该器件会带来与快慢通道相关的其它问题。

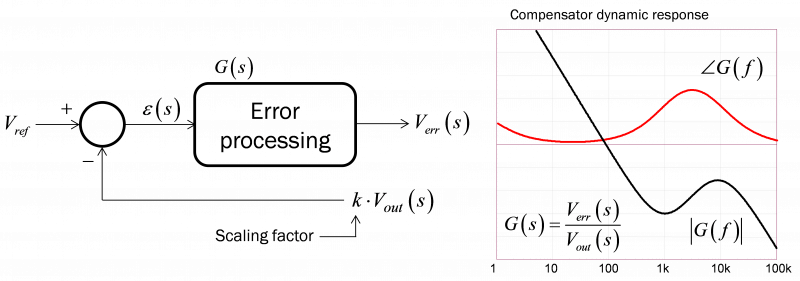
图 2: 您通过补偿器插入极点和零点并形成所需的频率响应。

此外，还可以选择使用跨导运算放大器(OTA)来达到补偿目的。集成电路设计人员喜欢使用 OTA，因为它们占用的硅芯片区域要少于对应的运算放大器。我个人不太喜欢 OTA，因为基于运算放大器的补偿器提供虚拟接地，而基于 OTA 的则没有。此外，电阻分压比也会影响极点 / 零点布局。

图 3:设计补偿器时有多种有源元件可供选择。

OTA 在功率因数校正(PFC)应用中比较受欢迎，非常适合用于实现具有适度相位边限提升的补偿器。如果您打算将其用于需要实现高相位边限提升的应用，则可能会达到 Vout/Vref 比例的上限。

相位边限提升是为满足相位裕度目标而需要补偿器补偿的额外相位量，通常为大于 45°的数字。通过图 4，您会发现功率级在某些选定频率 f1 和 f2 下具有 90°或 145°的相位滞后。如果使用具有 270°固定滞后的标准积分器来闭合环路，则这两个因素在 f1 频率下的滞后之和为 -360°或 0°：信号在注入点同相返回，并且满足持续振荡的条件。这并不是您想要的，除非您的目标就是构建一个振荡器。现在，如果您在 f2 频率下强制交越，则相位裕度为负数，也就是说闭环极点位于右半平面上：系统不稳定。您可以通过在 f1 或 f2 频率处实现相位边限提升来解决这个问题。通过将极点和零点放在补偿器中，您就可以调整其相位响应，使其不再固定为 -270°，而是更低的值。当与设备响应相结合时，总参数或相位现在将小于 -360°，从而获得实现稳定所需的相位裕度。

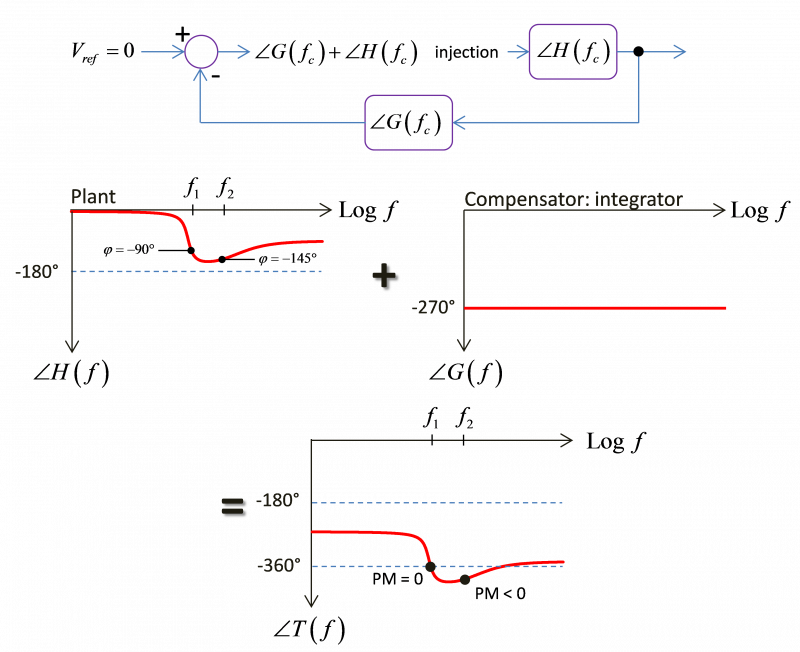
图 4：设备相位与补偿器相位相加应使得总相位滞后低于 -360°。

我们可以确定三种类型的补偿器，称为类型 1、2 和 3，如图 5 中所示。第 1 种类型包含原点极点：它是以下传递函数所表示的积分器：   

无相位边限提升，并且相位为反相运算放大器结构的相位(-180°)加上原点极点的相位(-90°)，因此最终参数为 -270°或 90°。

第 2 种类型常见于所需相位边限提升低于 90°的电流模式控制设计。它包含原点极点以及一个极点和一个零点。理论上，原点极点(s=0)可以消除静态误差（目标直流电源与环路闭合时的直流电源之间的偏差）。这种极点存在于绝大多数的补偿器中，但也有些技术（如所谓的输出电阻成形）会故意忽略这种极点并接受一点小偏差。

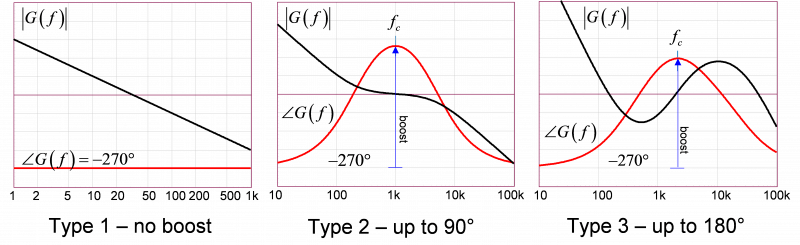
图 5 ： 您可以使用这三种配置实现补偿策略。

在第 2 种类型中，零点位于极点之前，会使相位随着频率升高而增加。极点在稍后出现，然后相位边限提升返回至零点。通过扩散零点和极点，您可以根据需要调整相位边限提升，最高可达 90°。请注意，如果将极点和零点重合，补偿器又会变成第 1 种类型，相位边限提升为 0°。

该结构中描述的传递函数如下所示：

您可以看到，分子中存在反向零点，因此可通过具有增益维度的 G0 进行因式分解。

最后，第 3 种类型的补偿器在第 2 种类型的基础上增加了另一对极点 - 零点，并且可将相位提升至最高 180°。这可以通过下述表达式进行描述：

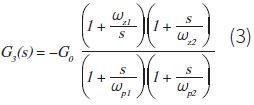
如果我们现在对 G(s)使用第 3 种类型的电路，而不是图 4 示例中的单纯积分器，并将相位提升 125°，那么目前的总环路相位会偏离 0°或 -360°，并且我们会具有 70°的裕度（图 6）。

根据功率级滞后和所需的相位裕度 jm，我们可以推导出一个与所需相位边限提升量相关的公式。我们都知道，反相运算放大器和原点上的极点会导致 270°滞后，再加上以选定交越频率 fc 表征的功率级相位。这些数字相加，结果应该就与 -360°限值相差相位裕量。因此，我们可以这样写：

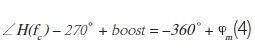
通过求解提升值，我们可以得到：

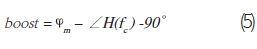
根据这个数字，我们可以推断出要使用的补偿器类型：
1. 无需提升：第 1 种类型。适用于不连续传导模式转换器，并且从某种程度上说，也适用于 PFC 级。
2. 最高 90°：第 2 种类型。常用于电流模式控制转换器（例如，反激和 PFC 级）。
3. 超过 90°但低于 180°：第 3 种类型。通常用于在连续传导模式(CCM)下运行的电压模式控制转换器。

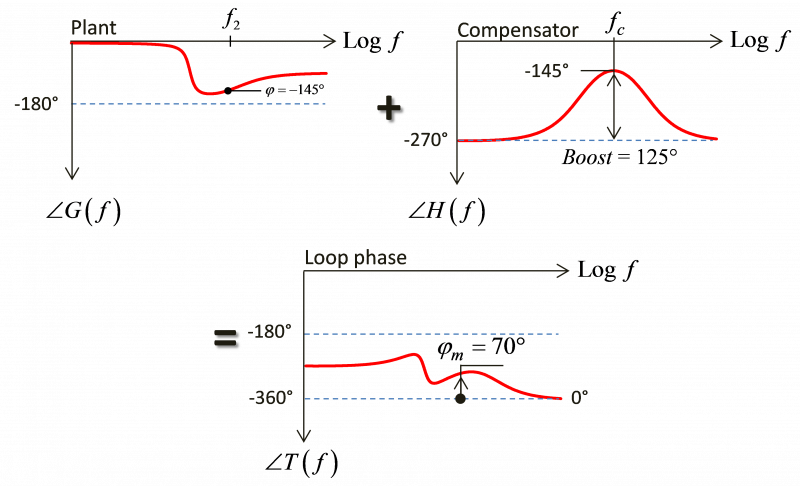
图 6： 相位裕度目前为 70°，因此考虑使用第 3 种类型的补偿器。