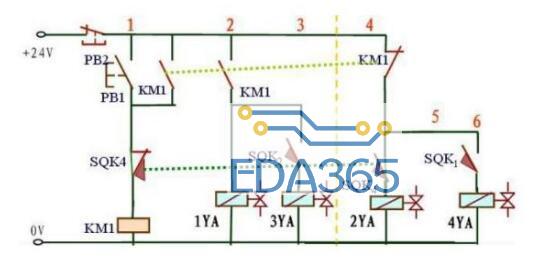
有块数字电路板需要对其轨电压去耦进行“最坏情况”分析，但挑战在于要确定最坏情况下的电流脉冲情况。
当前的任务是要表明，将轨电压传送到一块元器件稠密的电路板上时，其对于每安培电路板电流变化，不会经受超过40mV的瞬时漂移。上述变化(从10~90%和从90~10%)的上升和下降时间规定为不超过3ns。
分析的第一部分是要表征电流漂移。为此设计了两个模型：正弦半波和带位移余弦。如图1和图2所示，可以对这两种情况推导出脉冲轮廓的参数，从而产生3ns的上升时间和3ns的下降时间。
这两个脉冲模型之间的主要区别在于，正弦半波在电流流动的起止位置具有拐角，在这些地方一阶导数会发生突变；带位移余弦模型可以使这些过渡变得平滑，因此没有一阶导数突变。其结果很快就会显而易见。
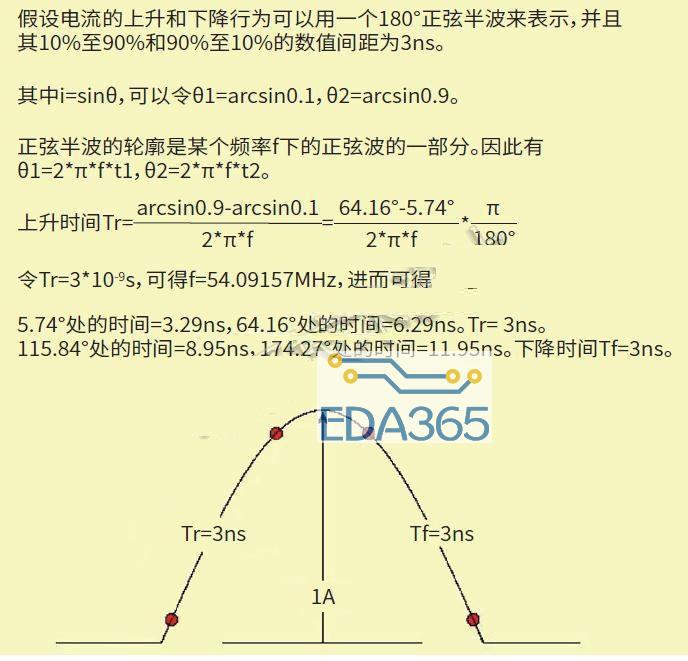
图1：正弦半波脉冲模型在电流的起止位置具有拐角，在这些地方一阶导数会发生突变。
图2：带位移余弦脉冲模型使过渡变得平滑，因此没有一阶导数突变。
把这两个脉冲模型重叠起来就会发现，尽管它们俩有所不同，但是确实彼此非常接近。
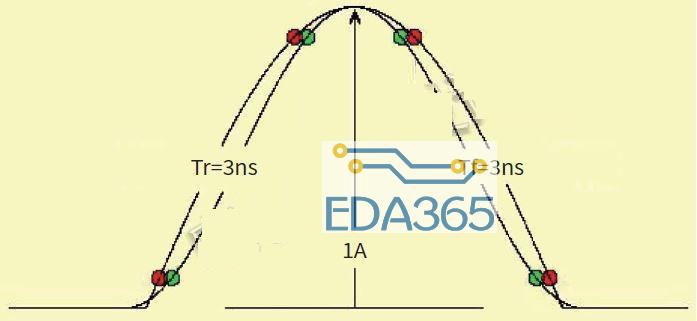
图3：两个脉冲模型非常接近。
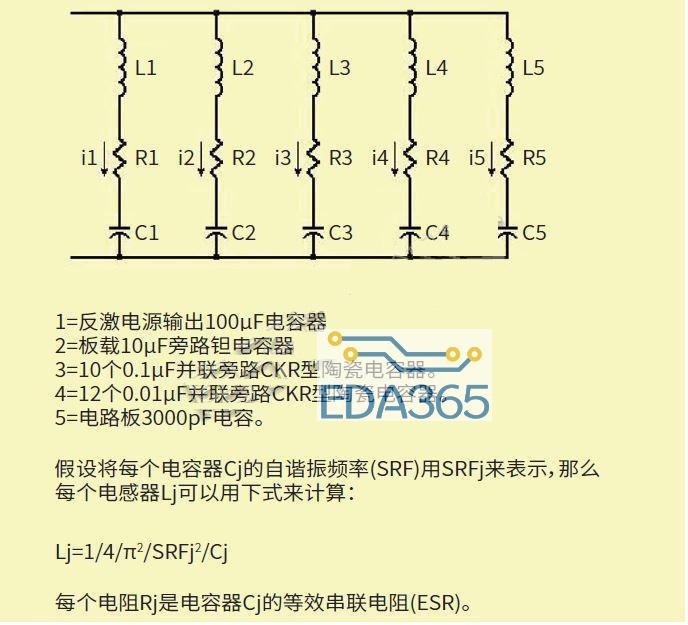
图4：电路板和电源电容器可以看作五个R、L、C的组合。
可以确定，+5V电源轨上的电容可以看作五个R、L、C的组合，其中有些是关于单个电容器，还有一些是关于多组电容器（图4）。性能分析方法是将符合所选脉冲模型的电流脉冲注入，然后使用递归微分方程检查图5所示的电压结果“e”。
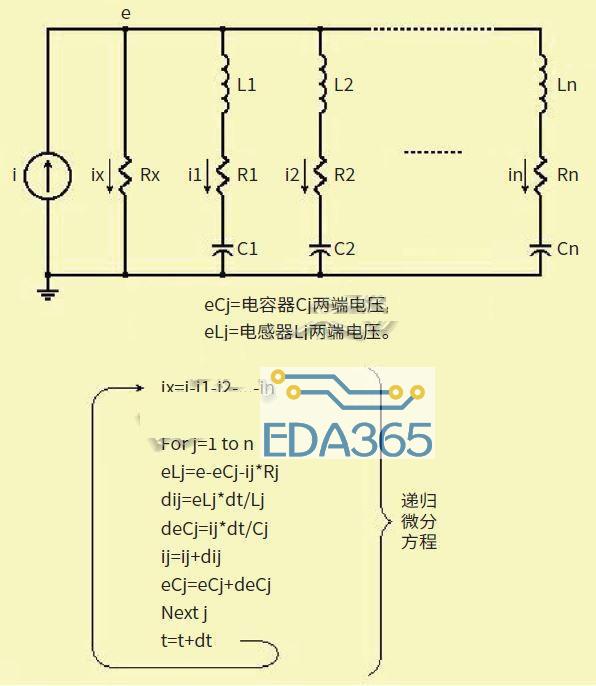
图5：用递归微分方程检查电压结果(本例中j=5)。
由于负载电流是从电容器组合中拉出，而不是将其灌入到这个组合，因此计算出的电压“e”必须要从+5V电源轨中减去。结果如图6所示。
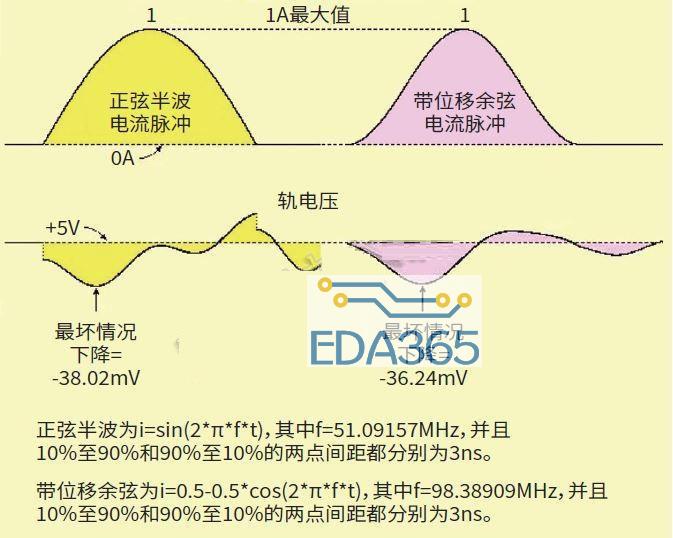
图6：从图中可知两种脉冲模型的轨电压漂移情况。
上述结果表明，两种电流脉冲模型均符合＜40mV的要求。值得注意的是，正弦半波模型的轨电压突变是由正弦半波不连贯的di/dt所引起，在现实世界中，这只是实际情况的近似值。
『本文转载自网络,版权归原作者所有,如有侵权请联系删除』
热门文章
更多
锂电池保护板作用_锂电池保护板怎么激活
APP下载
登录
