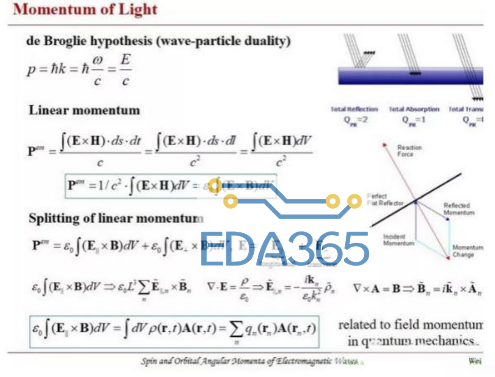
移动物体需要力。众所周知，速度随时间变化产生加速度；因而动量随时间变化，产生力。电磁系统也有力，比如电场力qE，磁场力qv x B。产生这些力对应的动量叫机械动量。但是，该机械动量并不是守恒量，一如电子-电磁耦合系统中电子的动量也不是守恒量一样。

如果把电磁场或光看成粒子，一如一颗颗子弹，它也能传递力至物体上。当电磁场经历镜面反射的时候，因为速度方向的改变，必然将动量传递给镜面，产生试图移动镜面的力。如果一束光被物体吸收，也有动量传递给该物体。如果物体足够小，足够轻，这种力是有可能移动物体的。这种场产生的动量，应该和电磁场的粒子性有某种联系。根据德布罗意假说，动量p = ℏk = ℏω/c = E/c。如果把能量写成功率和时间微分的乘积，功率写成能流密度E x H和面积微元dS的乘积，时间写成距离微元dl比上光速c，最终得到场动量密度表达式E x H / c2。而场动量加上机械动量是一个守恒量，它们共同产生的力，可用麦克斯韦应力张量来计算。这也是光力中最常用的计算方法。

如果进一步深入分析场动量的表达式，将会变得很有趣。在这个表达式中，如果将电场分解成纵向分量（近场、有源区）和横向分量（远场、无源区），纵向分量对应的项，∫v El x H / c2 dV，化简后居然是量子力学中对应的场动量qA。该场动量qA和电子动量mv加在一起是守恒量，被量子化后即正则动量算子。而剩下的横向分量，∫v Et x H / c2 dV，继续分解，又可以分成两项，一项是自旋动量，另一项是轨道动量。前者和电磁波的极化有关，圆极化带有自旋角动量。后者和电磁波的波前有关，涡旋电磁波（如高斯拉盖尔波束）带有轨道角动量。带有自旋角动量和轨道角动量的电磁波可以产生力矩，旋转粒子。电磁场中的自旋和轨道角动量的表达式和电子系统惊人的一致，除了自旋算子变成了3x3的Pauli矩阵而已。轨道动量密度和轨道角动量密度表达式正比于⟨E | -iℏ∇ | E⟩ 和⟨E | r x （-iℏ∇） | E⟩，这显然符合角动量算子的形式，L=r x p= r x （-iℏ∇）。

如果把轨道角动量空域表达式做傅里叶变换，得到k域表达式，k域的轨道动量密度不是别的，正是Berry Connection的定义。将Berry ConnecTIon沿着某闭合路径积分得到Berry Phase，除以2π就得到陈数。对圆极化的涡旋电磁波，该陈数联系到电磁波的自旋（σ = -1，1）和轨道（l = 1，-1，2，-2，…）拓扑电荷数之和。尽管涡旋波在自由空间通讯中遭遇模式串扰、波束发散、多径效应的困扰，它仍然是一个很稳定的波束，小的扰动不会改变其拓扑性质。而理解涡旋电磁波和拓扑绝缘体之间的联系，及轨道角动量通讯中如何挖掘涡旋电磁波的拓扑性质，是值得深入探索的课题。而从物理角度具有拓扑稳定的涡旋电磁波，在通讯工程上的实际应用仍需极大努力。“Even though many problems are a ‘done deal’ in the physics community， they are not a ‘done deal’ in an engineering community. Much blood， sweat， and tears are needed.”

上述观点，是作者个人的思考和体会，并不代表正确严格的电磁理论。欢迎大家批评指正！本文的数学公式（未发表），见如下图片。