运放补偿虽然很常见，但有时候也极具挑战性，尤其是在要求和约束条件超过设计师控制的情况下，设计师必须选择一种最优补偿技术之时。也许极具挑战性的原因之一是一般文献资料更多地专注于不同补偿技术之间的区别而不是相似性。

除了关注概念上的不同点外，还要关注相似点，这是非常明智的，只有这样才能更好地理解明显不同的技术和概念之间的紧密关系。为了达到这个目标，本文首先讨论了运放的少量几个确定因素，最终逐步过渡到电路中经常使用但少有人理解的补偿技术。本文还简要介绍了补偿网络的严格定义，并集中讨论了文献中出现的可能冲突。

前馈增益：相对于哪个节点？

在讨论运放补偿之前，首先搞清楚运放的两种最基本配置很重要，即同相（图1A）和反相（图1B）。已有大量文献资料介绍过这两种配置的闭环增益，并强调了闭环传输函数间的区别。

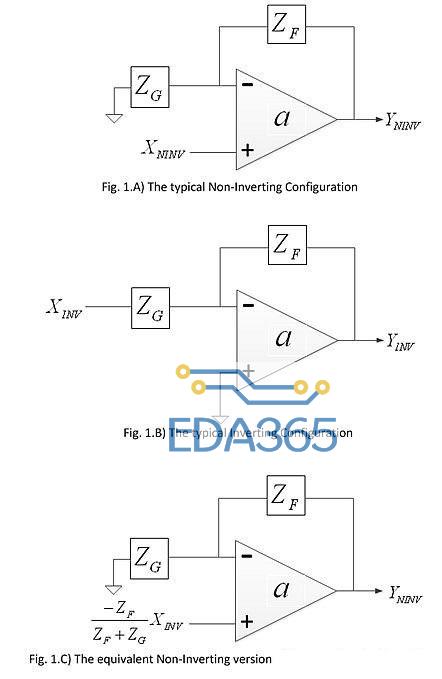
图1A：典型的同相配置。

图1B：典型的反相配置。

图1C：反相配置的等效同相版本。

为了方便理解两种配置的前馈增益之间的区别，这里给出了分别对应同相和反相配置的公式1.a和1.b。有人可能会问，为什么反相配置（AINV）的前馈增益不同于同相配置（ANINV），而事实上两种配置使用的是相同的运放。

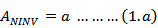
公式1.a

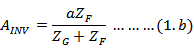
公式1.b

让我们首先看看两种配置实际上有多相似，然后说明前馈增益的纯数学表达式为何不同。

图1B中所示的反相配置可以转化为图1C所示的等效同相配置。这种转换是确定同相配置要求的输入后会产生与反相配置相同输出的结果。

图2A和图2B分别对应图1A和图1C的框图表示法。注意图2A和图2B之间的相似性。这两张图表明，当从减法模块向输出观察时，两种配置是完全相同的。减法模块建模的是运放两个输入端的相减。

在反相配置框图（图2B）中，输入信号（-XINV）先乘以ZF/（ZF+ZG）因子，然后到达减法模块输入端，命名为XINV，i。在图2A和图2B的两个框图之间，当严格相对于减法模块输入或运放输入观察时，前馈增益和反馈因子完全相同，两种配置的区别仅是相对输入信号观察时输入信号的数学转换。因此两种配置下的开环增益稳定性分析结果也是相同的。

通过使用线性系统处理方法，图2B中的反相配置框图可以映射为图2C。图2C中的框图是对反相配置进行简单数学处理的结果，不过图2B中的子模块更好地对应于实际物理系统的单元。与物理系统有更好的一对一对应关系的模型一般更容易让人理解。图2C是相对于信号源（-XINV）的反相配置的框图表示法，因此公式1.b中所示的前馈增益表达式（AINV）对同相配置来说看起来不同于公式1.a的表达式。

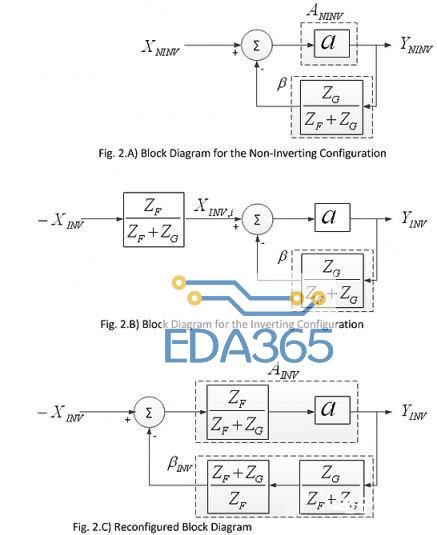
图2A：同相配置框图。

图2B：反相配置框图。

图2C：针对反相配置的重配置框图。

噪声增益：不仅仅针对噪声

为了方便理解，输出噪声（包括偏移量）通常以运放或放大器的输入端为参考。一般来说，给定极性的输出电压完全以运放正输入端为参考会导致输入电压与输出电压有相同的极性，而完全以负输入端为参考会导致相反极性的输入电压。

从非相关噪声模型角度看，噪声电压的符号或相位是不相关的，因此噪声电压的参考是运放的反相还是同相输入端在数学上都是等效的。由于反相输入端有反馈网络，因此输出噪声完全以运放的同相输入端为参考能够很快得出同相放大器的有效且可识别的配置（图1A）。这样，以运放任一输入端为参考的噪声总体增益总是等于反相配置的闭环增益。

因此，即使采用了相对于信号源的反相配置，但以运放输入端为参考的噪声实际上只看到等于（1+ZF/ZG）的同相配置增益，一般称之为噪声增益（NG）。然而，如果噪声源连接的是运放的正输入端，就像同相配置中那样，那么信号增益以及以输入为参考的噪声就完全等于噪声增益。

补偿技术：目的

运放补偿技术有很多种，如“主极点补偿”，“增益补偿”，“超前补偿”，“补偿衰减器”以及“超前-滞后补偿”。任何补偿技术的理想结果都是从纯稳定性角度使多极点系统（高阶系统）接近单极点整体系统，因为单极点反馈系统是无条件稳定的。

大多数补偿技术至少能实现有效的双极点系统状态，其中第二个极点（第一个非主要极点）尽可能远离第一个极点（主要极点），并且通常具有较高的频率拐点，而且拐点相对远，对稳定性的影响可以忽略不计。在一些情况下，通过有意减小主要极点和非主要极点之间的距离来增强带宽，这时通过增益频率响应可以观察到一些高频峰值。

在许多电子技术文献中，所有补偿技术中解释最不好的也许是超前-滞后补偿技术了。遗憾的是，某些流行的参考文献在开环增益曲线以及对超前-滞后补偿的相关描述中存在错误，因此本文将重点讨论这方面内容。

超前网络的严格定义或至少清晰的定义是，它的零点频率幅值比极点的要低，因此催生出纯粹两个拐点。在滞后网络中则相反，极点频率幅值比零点的低。超前-滞后网络是这两种网络的组合，超前网络的全部两个拐点频率的频率幅值都要小于滞后网络的频率幅值。同样，在滞后-超前网络中，滞后网络的两个拐点的频率幅值要小于超前网络。不管是滞后-超前网络还是超前-滞后网络，每种网络都会形成4个拐点：两个极点和两个零点。

在给定总体系统与技术约束条件下，人们也许会使用任何合适的补偿网络去补偿具有与生俱来且有时不可修改拐点的系统。所选的补偿技术可能专门用引入的零点去抵消固有的系统极点，反之亦然，从而得到一个纯粹更低阶的系统。本文采用开环增益表达式的Bode图用于稳定性分析，并得出极点和零点的定义。

超前-滞后补偿：实现

根据参考文献给出的超前-滞后补偿电路如图3A所示。出于实用和简单的目的，假设未补偿运放有两个固有极点：主极点（？p，dom）和第一个非主要极点（？p，nondom）。图3B显示了开环增益幅度图，其中实线代表未补偿运放的情况，显示出了运放本身的固有拐点。

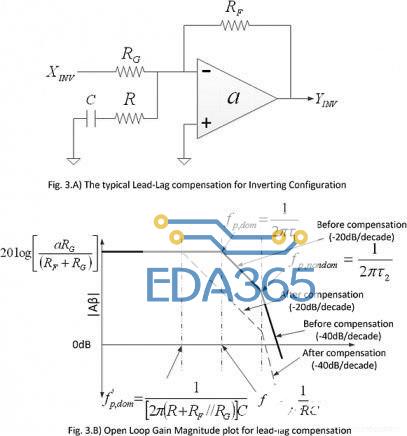
图3A：针对反相配置的典型超前-滞后补偿。

图3B：针对超前-滞后补偿的开环增益幅度图。

通过引入超前-滞后补偿而引入了一个极点（？’p，dom）和一个零点（？z），引入的极点（？’p，dom）变成了新的主极点，引入的零点（？z）基本上抵消了运放的固有主极点（？p，dom），虽然图3B显示的是？z 和？？p，dom之间完美的抵消。这样文献中所示的对应（错误的）图应该可以理解了。与许多其它补偿技术一样，超前-滞后补偿的一个明显优势是，所形成的主极点和非主极点之间的间距增加了，从而增强了稳定性。然而有人可能会问为何不是只执行超前补偿，用补偿网络引入的零点抵消运放固有的第一个非主要极点。

一个众所周知的原因是，超前补偿明显会产生带宽限制，而超前-滞后补偿不会。为什么超前-滞后补偿不会限制带宽呢？如果从开环增益曲线看全部可见的话，这个问题的答案不是很明确。有人也许通过分析闭环放大过程可以得到答案。针对超前-滞后补偿情况，另一篇文献很好地提出了闭环增益计算公式，但这里对这种技术为何不会限制带宽给出了一种直观的解释，虽然利用了一些简单的数学方法。

在图1所示的两个放大器配置中，运放的负输入端是负反馈点，因此只要在感兴趣频率点的开环增益幅度足够大，这就是一个非常低的增量阻抗节点，也称为虚地。所以将信号源电压转换为等效输入信号电流、然后乘上反馈电阻值（RF）得到纯输出电压（YINV）是有意义的，如图4所示。

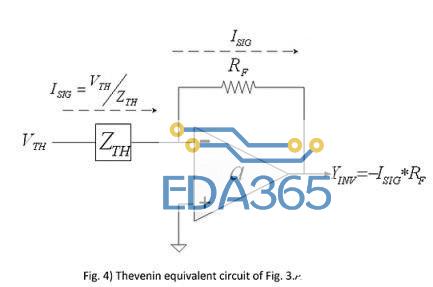
图4：图3A的戴文宁等效电路。

完成这种转换的一种流行方法是通过戴文宁等效网络。图4显示了图3A的戴文宁等效电路。在图3A中，假设运放及其反馈网络不存在，换句话说去除了负载，然后考虑在以前连接的运放负输入端处来自输入源（XINV）的贡献。这种贡献可以被称作戴文宁等效电压（VTH），它的幅度随频率增加而减小，因为当频率增加时补偿电容的阻抗会减小。

与此同时，由于补偿电容的作用，戴文宁等效串联阻抗（ZTH）受相同方式的影响。因此流向运放负输入端（虚地）的净信号电流（ISIG）将等于（VTH/ZTH=XINV/RG），其中分子项VTH中的所有拐点将被分母项ZTH中的所有拐点所抵消，继而导致不受补偿网络影响的信号电流。最终由于超前-滞后网络的使用而没有带宽限制。见公式2a和公式2b。

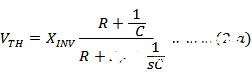
公式2.a

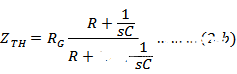
公式2.b

这种超前-滞后实现的缺点是，随着频率的变化会出现噪声增益峰值，但只要有足够的补偿，信号路径增益就不会出现峰值，因而降低了信噪比（SNR）。

超前补偿：不同实现方法

至此讨论的超前-滞后补偿（图3A）的实现方法是，在运放负输入端到地之间、或等效在运放两个输入端之间连接串联电阻和电容元件。然而，当这样的串联结构连接在放大晶体管的输入-输出引脚之间时，补偿技术被称为超前补偿与最终极点分离补偿的组合。这种串联电阻与电容补偿结构几乎总是存在于运放内部。

通常这个过程一开始是在增益单元间放置一个电容，这样由于电容米勒效应会形成极点分离补偿。然后为了补偿由此形成的右半平面零点，需要增加一个串联电阻，并通过调整阻值实现超前补偿，此时需要移动零点直到它抵消第一个非主要极点。最终人们如何连接这样的串联电阻和电容网络取决于超前或超前-滞后补偿顶点的具体要求和可用选项。

为了在使用运放IC的放大器中实现超前补偿，需要并联反馈电阻放置一个反馈电容。尽管是超前补偿实现方法，但它的意图通常是通过补偿网络引入一个零点来抵消一个极点，而且一般是待补偿系统的第一个非主要极点。

结束语

按照文献中描述的补偿网络严格定义，图3A中所示的所谓超前-滞后补偿从严格意义上讲是一种滞后补偿。同样，在晶体管放大节点间放置的所谓超前补偿网络，严格来说也是一种滞后补偿网络。这再一次提醒人们这些补偿技术实际上有多相似，而在不同参考文献中基于这样那样的理由却被分成不同的种类。也许除了“增益补偿”技术外，所有上面提及的补偿技术都可以归类为“拐点补偿”技术，因为直流开环增益幅度在补偿过程中保持恒定，只有拐点会经历重新定位、创建和消除的组合过程。