本系列文章共有三部分,“第 1 部分”重点介绍如何准确地估算某个时钟源的抖动,以及如何将其与 ADC 的孔径抖动组合。在“第 2 部分”中,该组合抖动将用于计算 ADC 的 SRN,然后将其与实际测量结果对比。“第 3 部分”将介绍如何通过改善 ADC 的孔径抖动来进一步增加 ADC 的 SNR,并会重点介绍时钟信号转换速率的优化。
第 1 部分 重点介绍如何准确地估算某个时钟源的抖动,以及如何将其与 ADC 的孔径抖动组合(如下)
采样过程回顾
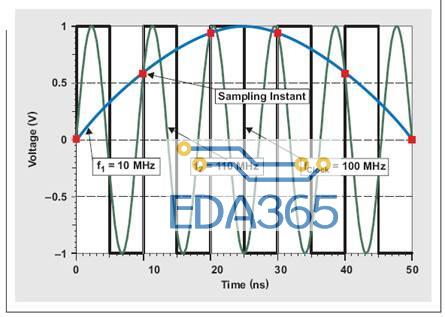
根据 Nyquist-Shannon 采样定理,如果以至少两倍于其最大频率的速率来对原始输入信号采样,则其可以得到完全重建。假设以 100 MSPS 的速率对高达 10MHz 的输入信号采样,则不管该信号是位于 1 到 10MHz 的基带(首个Nyquist 区域),还是在 100 到 110MHz 的更高 Nyquist 区域内欠采样,都没关系(请参见图 1)。在更高(第二个、第三个等)Nyquist 区域中采样,一般被称作欠采样或次采样。然而,在 ADC 前面要求使用抗混叠过滤,以对理想 Nyquist 区域采样,同时避免重建原始信号过程中产生干扰。
图 1 100MSPS 采样的两个输入信号显示了混叠带来的相同采样点
时域抖动
仔细观察某个采样点,可以看到计时不准(时钟抖动或时钟相位噪声)是如何形成振幅变化的。由于高 Nyquist 区域(例如,f1 = 10 MHz 到 f2 = 110 MHz)欠采样带来输入频率的增加,固定数量的时钟抖动自理想采样点产生更大数量的振幅偏差(噪声)。另外,图 2 表明时钟信号自身转换速率对采样时间的变化产生了影响。转换速率决定了时钟信号通过零交叉点的快慢。换句话说,转换速率直接影响 ADC 中时钟电路的触发阈值。
图 2 时钟抖动形成更多快速输入信号振幅误差

如果 ADC 的内部时钟缓冲器上存在固定数量的热噪声,则转换速率也转换为计时不准,从而降低了 ADC 的固有窗口抖动。如图 3 所示,窗口抖动与时钟抖动(相位噪声)没有一点关系,但是这两种抖动分量在采样时间组合在一起。图 3 还表明窗口抖动随转换速率降低而增加。转换速率一般直接取决于时钟振幅。

时钟抖动导致的 SNR 减弱
有几个因素会限制 ADC 的 SNR,例如:量化噪声(管线式转换器中一般不明显)、热噪声(其在低输入频率下限制 SNR),以及时钟抖动(SNRJitter)(请参见下面方程式 1)。SNRJitter 部分受到输入频率 fIN(取决于 Nyquist 区域)的限制,同时受总时钟抖动量 tJitter 的限制,其计算方法如下:

SNRJitter[dBc]=-20×log(2π×fIN×tJitter)uf8f9uf8fb(2)
正如我们预计的那样,利用固定数量的时钟抖动,SNR 随输入频率上升而下降。图 4 描述了这种现象,其显示了 400 fs 固定时钟抖动时一个 14 位管线式转换器的 SNR。如果输入频率增加十倍,例如:从 10MHz 增加到 100MHz,则时钟抖动带来的最大实际 SNR 降低 20dB。

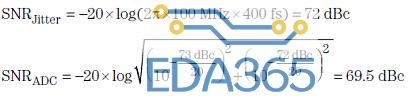
如前所述,限制 ADC SNR 的另一个主要因素是 ADC 的热噪声,其不随输入频率变化。一个 14 位管线式转换器一般有 ~70 到 74 dB 的热噪声,如图 4 所示。我们可以在产品说明书中找到 ADC 的热噪声,其相当于最低指定输入频率(本例中为 10MHz)的 SNR,其中时钟抖动还不是一个因素。
让我们来对一个具有 400 fs 抖动时钟电路和 ~73 dB 热噪声的 14 位 ADC 进行分析。低输入频率(例如:10MHz 等)下,该 ADC 的 SNR 主要由其热噪声定义。由于输入频率增加,400-fs 时钟抖动越来越占据主导,直到 ~300 MHz 时完全接管。尽管相比 10MHz 的 SNR,100MHz 输入频率下时钟抖动带来的 SNR 每十倍频降低 20dB,但是总 SNR 仅降低 ~3.5 dB(降至 69.5dB),因为存在 73-dB 热噪声(请参见图 5):
现在,很明显,如果 ADC 的热噪声增加,对高输入频率采样时时钟抖动便非常重要。例如,一个 16 位 ADC 具有 ~77 到 80 dB 的热噪声层。根据图 4 所示曲线图,为了最小化 100MHz 输入频率 SNR 的时钟抖动影响,时钟抖动需为大约 150 fs 或更高。

 APP下载
APP下载 登录
登录














 热门文章
热门文章