1. 加法器，减法器都是从一位的二进制数开始进行例题讲解，逐渐扩展到多位二进制位数之间的运算。在设计逻辑电路的过程中，根据所描述的功能构建好真值表。出题者喜欢要求读者用与或门，与或非门构建函数表达式。它的原因在于依据真值表写函数表达式，最标准的就是最小项表达式。以下小图的逻辑图来看与或门，我们的头脑中不能老是思维定势，认为输入就是两个，在实际生活中，输入应该非常多，远非两个，在逻辑符号中，要清楚地认识与非门的多输入的画法，将与门分成了好几格，每一格代表一个与门电路。下小图可以写成 AB+CD+EF（不认真考虑前面的输入），由细小的门集成为更大的门，将某一部分单独来看，它们就是一个整体，如（AB+CD+EF），体现在逻辑图中就是一个角。

如果从全图的角度看，在最后一级门电路中，每一个小整体代表着输出。最后一级的与门中，有两个输入，有三个输入，这都是可以的，最多输入的个数是依照初始的输入的个数来定，不可能超过这个数，只可能少于这个数，因为对于某一输出而言，并非所有的输入对它都是有效的。从最左边的所有输入，经过逻辑电路图，在最右边得到了所有的输出。还有一点，这是与或表达式的逻辑图，如果在写逻辑表达式，包括化简变化函数式时，采用了不同于与或形式的表达式，那么最终得到的逻辑图就和下面的与或形式的逻辑图完全不一样。

2. 一位的全减器是指，两个一位的二进制数之间进行减法运算。全减器的特例就是半减器。

多位二进制减法器，是由加法电路构成的；在加法电路的基础上，减法与加法采用同一套电路，实现加减法共用。

3. 这里的多位二进制数的减法，是指无符号数，为什么？

将减法运算转换为加法运算，采用的是补数的方法完成的。这就解释了为什么两者能共用一套电路，是不是减法在转换时，我们需要在加法电路的基础上进行一些小的扩展，来进行减法的补码转换？

N 反是每一位都取反，没有符号位，下式当中，A-B 是减法，通过形式转化，将 -B 化为 B 反+1-2n，B 是正数，A 和 B 均为无符号数，通过补码的转变，我们成功的将 -B 变为了固定的 -2n，但是这还是有减号，该怎么解决？

仔细观察下面这张图，A 和 B 是两个四位二进制数相减。A 的四位是正常输入，B 的输入是取反输入，低位向高位的进位 C-1 的作用是输入 1，这样就完成了 A+B 反+1，至于 -2n，我们是通过本想向高位的输入来实现的，对 CO 输出取反，就是 -2n，如果 V 输出是 1，代表 A 小于 B，产生了借位，如果 V 输出为 0，则 A 大于 B，不用借位。为什么 -2n 是这样实现的？原理是什么？V 是一种输出，应该有相应的表达式。有进位的话，进位再取反，没有的话，怎么办？通过实际的例子，我们发现，本位向高位的进位一直是有的，要么是 1，要么是 0，没有进位就是 0。

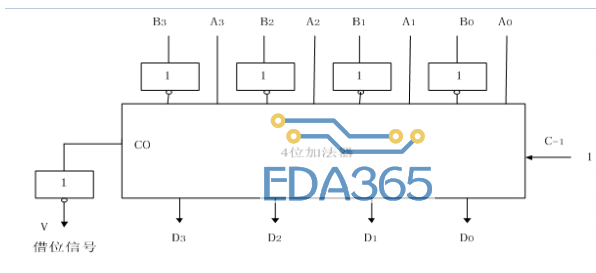
这里对于补码，反码的概念不是很清楚。

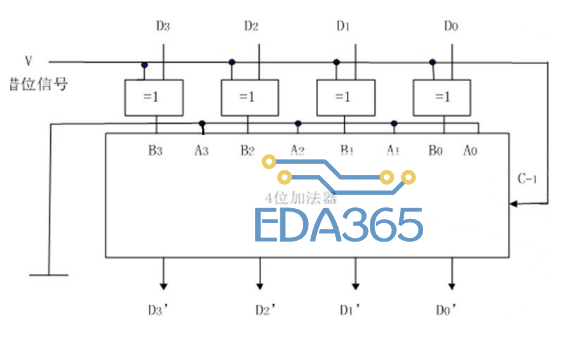
如果是 A-B，A 小于 B，那么通过加法器算出来的结果，还需要再次求反（不包括借位位的输出），加 1，这就涉及再次取反电路的设计，原先的进位位的取反已经算是对加法器做了改变。下图就是结果再取反的逻辑图：V 的借位信号是 1 时，V 和 D3 的异或，将 V 和 D3 都当作自变量 1，那么输出肯定是 0，0 可以用 D3‘来代替，同时，V 为 1 的信号还要当成低位向本位的进位，输入 1，为了充分的利用加法器，我们必须将 A 的输入端全部接地，这个器件实际上是为 V 为 1 研究设计的，如果 V 为 0 输入时，0 和 D3 异或时，D3 当作 1 来看，输出为 1，就是 D3，此时，C-1 输入也为 0

4. 讲解过四位二进制加法电路和四位二进制减法电路，如何设计两个四位加减共用电路，输入信号里面要提供一个加还是减的信号，到底如何设定？

5. 四位全加器电路除了实现加法的功能，还有什么应用。

用四位全加器实现 8421BCD 码到余 3BCD 码的转换。

用四位全加器来将输入的余 3BCD 码转化成 BCD 码，可以有两种方法，第一种是余 3BCD 直接减 3，另一种是余 3BCD 加 13，这是为什么？