1）不完全微分PID算法。在PID控制中，微分信号的引入可改善系统的动态特性，但也易引起高频干扰，在误差扰动突变时尤其显出微分项的不是。若在控制算法中加人低通滤波器，则可使系统性能得到改善。克服上述缺点的方法之一，是在PID算法中加入一个一阶惯性环节（低通滤波器）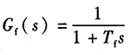
,可使系统性能得到改善。
不完全微分PID的结构如图所示，其中图a是将低通滤波器直接加在微分环节上。本系统采用图a的方法，可以有效抑制干扰信号的影响，改善系统性能。
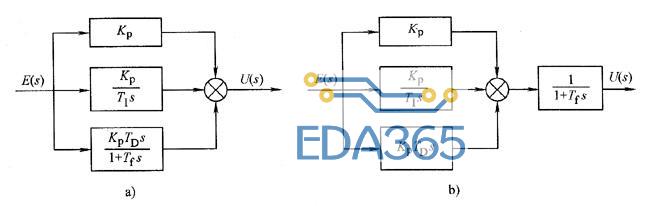
图 不完全微分PID结构
2）积分饱和及抑制。在实际过程中，控制变量乙因受到执行元件机械和物理性能的约束而控制在有限范围内，即umin≤u（k）≤umax。如果由计算机给出的控制量形在上述范围内，那么控制可以按预期的结果进行。一旦超出上述范围，那么实际执行的控制量就不再是计算值，由此将引起不期望的效应。
①遇限削弱积分法。一旦控制变量进入饱和区，将只执行削弱积分项的运算而停止进行增大积分项的运算。具体地说，在计算u（k）时，将判断上一时刻的控制量u（k）是否已超出限制范围。如果已超出，那么将根据偏差的符号，判断系统输出是否在超调区域，由此决定是否将相应偏差计人积分项。在三闭环控制程序的速度环中就应用了这个方法。
②积分分离法。减小积分饱和的关键在于不能使积分项累积过大。上面的修正方法是一开始就积分，但进人限制范围后即停止累积。这里介绍的积分分离法正好与其相反，它在开始时不进行积分，直到偏差达到一定的阈值后才进行积分累计。这样，一方面防止了一开始有过大的控制量；另一方面即使进入饱和后，因积分累积小，也能较快退出，减少了超调。
『本文转载自网络,版权归原作者所有,如有侵权请联系删除』
热门文章
更多
如何使用protel电路设计软件设计高速PCB
APP下载
登录
