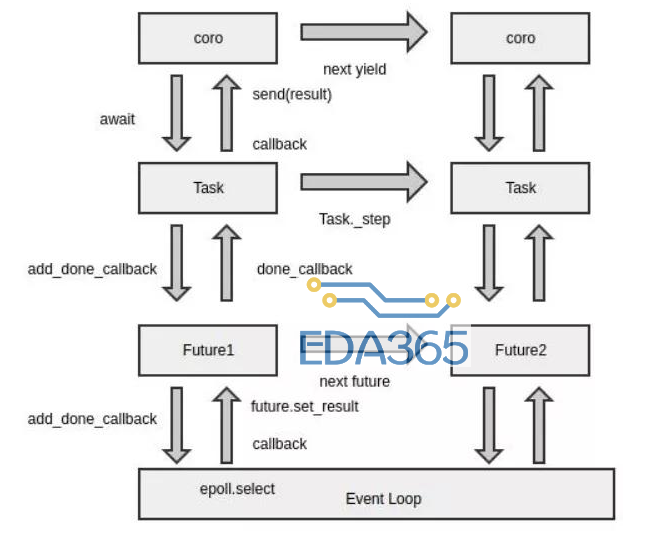
本文采用C++中的vector实现栈结构，然后利用栈实现判断平衡符号，实现中缀表达式到后缀表达式的转换，并依据栈实现简单的整数加减乘除运算。

首先栈的实现，由于在C++中采用了vector来代替原始的数组操作，这种比较方便的容器能较好的实现数组的功能，当然栈也可以采用链表实现，但是我认为链表没有数组直观，而且在实际的计算机里也是采用连续的存储空间作为栈空间的，因此选择Vector。主要实现三个操作，push、pop以及为空判断。基本的形式如下：

#ifndef __MYSTACK_H_H_
#define __MYSTACK_H_H_

#include "myvector.h"

namespace myspace
{
template
class Stack
{
public:
Stack(){}
void push(const Object &x)
{
objects.push_back(x);
}

const Object &pop()
{
int len;
if(!isempty())
{
objects.pop_back();
len = objects.size();
return objects[len];
}
}

bool isempty()const
{
return (objects.size() == 0);
}

int size()
{
return objects.size();
}
private:
Vector

#endif

实现了简单的栈类，接下来采用栈实现一些简单的运用。

符号的平衡问题
在语言中往往需要判断一些符号是否是成对出现的，比如<>,{},[],()，通常在C++中也只有这几种对称问题，如何让判断符号的对称也是很多代码判断的首要任务。当然实现的方式是多种多样的，采用栈的实现会相对更加简单。基本的实现思路如下：
假设在读入一串字符串以后，如果遇到对称符号的左边部分，则将其压入栈中，当遇到对称符号的右边部分，则弹出栈中的一个对象，实现比对，如果是对称的，则说明当前的符号是平衡的，如果不对称，则说明当前字符串是不平衡的，当字符串读完以后，如果所有的符号都是平衡的，栈中此时应该就是为空，通过判断栈中是否为空，说明字符串是否是符号平衡的。
依据上面实现的栈类，实现符号平衡判断的过程比较简单，如下所示：

bool isbalance(const string &str)
{
string::size_type len = str.size();

Stack stack;

for(string::size_type i = 0; i < len ; ++ i)
{
/*first selection*/
if(str[i] == [ || str[i] == { ||
str[i] == ( || str[i] == {
stack.push(str[i]);
}
/*如果是对称的符号，则从栈中弹出*/
if(str[i] == ] || str[i] == } ||
str[i] == ) || str[i] == >)
{
/*如果栈中没有对象，则说明不平衡*/
if(stack.isempty())
{
cout << "the string is Unblanced" << endl;
return false;
}
/*采用switch-case语句判断*/
switch(str[i])
{
case ]:
{
/*判断是否是匹配的*/
if([ != stack.pop())
{
cout << "Can not blanced with ]" << endl;
return false;
}
break;
}
case ):
{
if(( != stack.pop())
{
cout << "Can not blanced with )" << endl;
return false;
}
break;
}
case }:
{
if({ != stack.pop())
{
cout << "Can not blanced with }" << endl;
return false;
}
break;
}
case >:
{
if(< != stack.pop())
{
cout << "Can not blanced with >" << endl;
return false;
}
break;
}
/*一般的非对称字符*/
default:
break;
}
}
}